使用 PointNet 进行点云分割
作者： Soumik Rakshit, Sayak Paul
创建日期 2020/10/23
最后修改 2020/10/24
描述： 基于 PointNet 的点云分割模型实现。
简介
“点云”是一种用于存储几何形状数据的重要数据结构。由于其不规则的格式，在深度学习应用中使用之前，通常会将其转换为规则的 3D 体素网格或图像集合，这一步会使数据变得不必要地庞大。PointNet 系列模型通过直接使用点云解决了这个问题，尊重了点数据的置换不变性。PointNet 系列模型为从对象分类、零件分割到场景语义解析等应用提供了一个简单、统一的架构。
在此示例中，我们将演示 PointNet 架构在形状分割中的实现。
参考文献
导入
import os
import json
import random
import numpy as np
import pandas as pd
from tqdm import tqdm
from glob import glob
import tensorflow as tf # For tf.data
import keras
from keras import layers
import matplotlib.pyplot as plt
下载数据集
ShapeNet 数据集是一个持续努力建立一个富含注释的大规模 3D 形状数据集。ShapeNetCore 是完整 ShapeNet 数据集的一个子集，包含干净的单个 3D 模型以及手动验证的类别和对齐注释。它涵盖了 55 个常见的对象类别，大约有 51,300 个独特的 3D 模型。
在此示例中，我们使用 PASCAL 3D+ 的 12 个对象类别之一，该类别包含在 ShapenetCore 数据集中。
dataset_url = "https://git.io/JiY4i"
dataset_path = keras.utils.get_file(
fname="shapenet.zip",
origin=dataset_url,
cache_subdir="datasets",
hash_algorithm="auto",
extract=True,
archive_format="auto",
cache_dir="datasets",
)
加载数据集
我们解析数据集元数据，以便轻松地将模型类别映射到它们各自的目录，并将分割类别映射到颜色，以便进行可视化。
with open("/tmp/.keras/datasets/PartAnnotation/metadata.json") as json_file:
metadata = json.load(json_file)
print(metadata)
{'Airplane': {'directory': '02691156', 'lables': ['wing', 'body', 'tail', 'engine'], 'colors': ['blue', 'green', 'red', 'pink']}, 'Bag': {'directory': '02773838', 'lables': ['handle', 'body'], 'colors': ['blue', 'green']}, 'Cap': {'directory': '02954340', 'lables': ['panels', 'peak'], 'colors': ['blue', 'green']}, 'Car': {'directory': '02958343', 'lables': ['wheel', 'hood', 'roof'], 'colors': ['blue', 'green', 'red']}, 'Chair': {'directory': '03001627', 'lables': ['leg', 'arm', 'back', 'seat'], 'colors': ['blue', 'green', 'red', 'pink']}, 'Earphone': {'directory': '03261776', 'lables': ['earphone', 'headband'], 'colors': ['blue', 'green']}, 'Guitar': {'directory': '03467517', 'lables': ['head', 'body', 'neck'], 'colors': ['blue', 'green', 'red']}, 'Knife': {'directory': '03624134', 'lables': ['handle', 'blade'], 'colors': ['blue', 'green']}, 'Lamp': {'directory': '03636649', 'lables': ['canopy', 'lampshade', 'base'], 'colors': ['blue', 'green', 'red']}, 'Laptop': {'directory': '03642806', 'lables': ['keyboard'], 'colors': ['blue']}, 'Motorbike': {'directory': '03790512', 'lables': ['wheel', 'handle', 'gas_tank', 'light', 'seat'], 'colors': ['blue', 'green', 'red', 'pink', 'yellow']}, 'Mug': {'directory': '03797390', 'lables': ['handle'], 'colors': ['blue']}, 'Pistol': {'directory': '03948459', 'lables': ['trigger_and_guard', 'handle', 'barrel'], 'colors': ['blue', 'green', 'red']}, 'Rocket': {'directory': '04099429', 'lables': ['nose', 'body', 'fin'], 'colors': ['blue', 'green', 'red']}, 'Skateboard': {'directory': '04225987', 'lables': ['wheel', 'deck'], 'colors': ['blue', 'green']}, 'Table': {'directory': '04379243', 'lables': ['leg', 'top'], 'colors': ['blue', 'green']}}
在此示例中，我们训练 PointNet 来分割Airplane模型的各个部分。
points_dir = "/tmp/.keras/datasets/PartAnnotation/{}/points".format(
metadata["Airplane"]["directory"]
)
labels_dir = "/tmp/.keras/datasets/PartAnnotation/{}/points_label".format(
metadata["Airplane"]["directory"]
)
LABELS = metadata["Airplane"]["lables"]
COLORS = metadata["Airplane"]["colors"]
VAL_SPLIT = 0.2
NUM_SAMPLE_POINTS = 1024
BATCH_SIZE = 32
EPOCHS = 60
INITIAL_LR = 1e-3
构建数据集
我们从飞机点云及其标签生成以下内存数据结构
point_clouds是一个np.array对象列表，以 x、y 和 z 坐标的形式表示点云数据。轴 0 表示点云中点的数量，而轴 1 表示坐标。all_labels是表示每个坐标标签的字符串列表（主要用于可视化目的）。test_point_clouds的格式与point_clouds相同，但没有相应的点云标签。all_labels是一个np.array对象列表，表示每个坐标的点云标签，对应于point_clouds列表。point_cloud_labels是一个np.array对象列表，表示每个坐标的点云标签，以 one-hot 编码形式，对应于point_clouds列表。
point_clouds, test_point_clouds = [], []
point_cloud_labels, all_labels = [], []
points_files = glob(os.path.join(points_dir, "*.pts"))
for point_file in tqdm(points_files):
point_cloud = np.loadtxt(point_file)
if point_cloud.shape[0] < NUM_SAMPLE_POINTS:
continue
# Get the file-id of the current point cloud for parsing its
# labels.
file_id = point_file.split("/")[-1].split(".")[0]
label_data, num_labels = {}, 0
for label in LABELS:
label_file = os.path.join(labels_dir, label, file_id + ".seg")
if os.path.exists(label_file):
label_data[label] = np.loadtxt(label_file).astype("float32")
num_labels = len(label_data[label])
# Point clouds having labels will be our training samples.
try:
label_map = ["none"] * num_labels
for label in LABELS:
for i, data in enumerate(label_data[label]):
label_map[i] = label if data == 1 else label_map[i]
label_data = [
LABELS.index(label) if label != "none" else len(LABELS)
for label in label_map
]
# Apply one-hot encoding to the dense label representation.
label_data = keras.utils.to_categorical(label_data, num_classes=len(LABELS) + 1)
point_clouds.append(point_cloud)
point_cloud_labels.append(label_data)
all_labels.append(label_map)
except KeyError:
test_point_clouds.append(point_cloud)
100%|██████████████████████████████████████████████████████████████████████| 4045/4045 [01:30<00:00, 44.54it/s]
接下来，我们看一下刚刚生成的内存数组中的一些样本
for _ in range(5):
i = random.randint(0, len(point_clouds) - 1)
print(f"point_clouds[{i}].shape:", point_clouds[0].shape)
print(f"point_cloud_labels[{i}].shape:", point_cloud_labels[0].shape)
for j in range(5):
print(
f"all_labels[{i}][{j}]:",
all_labels[i][j],
f"\tpoint_cloud_labels[{i}][{j}]:",
point_cloud_labels[i][j],
"\n",
)
point_clouds[333].shape: (2571, 3)
point_cloud_labels[333].shape: (2571, 5)
all_labels[333][0]: tail point_cloud_labels[333][0]: [0. 0. 1. 0. 0.]
all_labels[333][1]: wing point_cloud_labels[333][1]: [1. 0. 0. 0. 0.]
all_labels[333][2]: tail point_cloud_labels[333][2]: [0. 0. 1. 0. 0.]
all_labels[333][3]: engine point_cloud_labels[333][3]: [0. 0. 0. 1. 0.]
all_labels[333][4]: wing point_cloud_labels[333][4]: [1. 0. 0. 0. 0.]
point_clouds[3273].shape: (2571, 3)
point_cloud_labels[3273].shape: (2571, 5)
all_labels[3273][0]: body point_cloud_labels[3273][0]: [0. 1. 0. 0. 0.]
all_labels[3273][1]: body point_cloud_labels[3273][1]: [0. 1. 0. 0. 0.]
all_labels[3273][2]: tail point_cloud_labels[3273][2]: [0. 0. 1. 0. 0.]
all_labels[3273][3]: wing point_cloud_labels[3273][3]: [1. 0. 0. 0. 0.]
all_labels[3273][4]: wing point_cloud_labels[3273][4]: [1. 0. 0. 0. 0.]
point_clouds[929].shape: (2571, 3)
point_cloud_labels[929].shape: (2571, 5)
all_labels[929][0]: body point_cloud_labels[929][0]: [0. 1. 0. 0. 0.]
all_labels[929][1]: tail point_cloud_labels[929][1]: [0. 0. 1. 0. 0.]
all_labels[929][2]: wing point_cloud_labels[929][2]: [1. 0. 0. 0. 0.]
all_labels[929][3]: tail point_cloud_labels[929][3]: [0. 0. 1. 0. 0.]
all_labels[929][4]: body point_cloud_labels[929][4]: [0. 1. 0. 0. 0.]
point_clouds[496].shape: (2571, 3)
point_cloud_labels[496].shape: (2571, 5)
all_labels[496][0]: body point_cloud_labels[496][0]: [0. 1. 0. 0. 0.]
all_labels[496][1]: body point_cloud_labels[496][1]: [0. 1. 0. 0. 0.]
all_labels[496][2]: body point_cloud_labels[496][2]: [0. 1. 0. 0. 0.]
all_labels[496][3]: wing point_cloud_labels[496][3]: [1. 0. 0. 0. 0.]
all_labels[496][4]: body point_cloud_labels[496][4]: [0. 1. 0. 0. 0.]
point_clouds[3508].shape: (2571, 3)
point_cloud_labels[3508].shape: (2571, 5)
all_labels[3508][0]: body point_cloud_labels[3508][0]: [0. 1. 0. 0. 0.]
all_labels[3508][1]: body point_cloud_labels[3508][1]: [0. 1. 0. 0. 0.]
all_labels[3508][2]: body point_cloud_labels[3508][2]: [0. 1. 0. 0. 0.]
all_labels[3508][3]: body point_cloud_labels[3508][3]: [0. 1. 0. 0. 0.]
all_labels[3508][4]: body point_cloud_labels[3508][4]: [0. 1. 0. 0. 0.]
现在，让我们可视化一些点云及其标签。
def visualize_data(point_cloud, labels):
df = pd.DataFrame(
data={
"x": point_cloud[:, 0],
"y": point_cloud[:, 1],
"z": point_cloud[:, 2],
"label": labels,
}
)
fig = plt.figure(figsize=(15, 10))
ax = plt.axes(projection="3d")
for index, label in enumerate(LABELS):
c_df = df[df["label"] == label]
try:
ax.scatter(
c_df["x"], c_df["y"], c_df["z"], label=label, alpha=0.5, c=COLORS[index]
)
except IndexError:
pass
ax.legend()
plt.show()
visualize_data(point_clouds[0], all_labels[0])
visualize_data(point_clouds[300], all_labels[300])
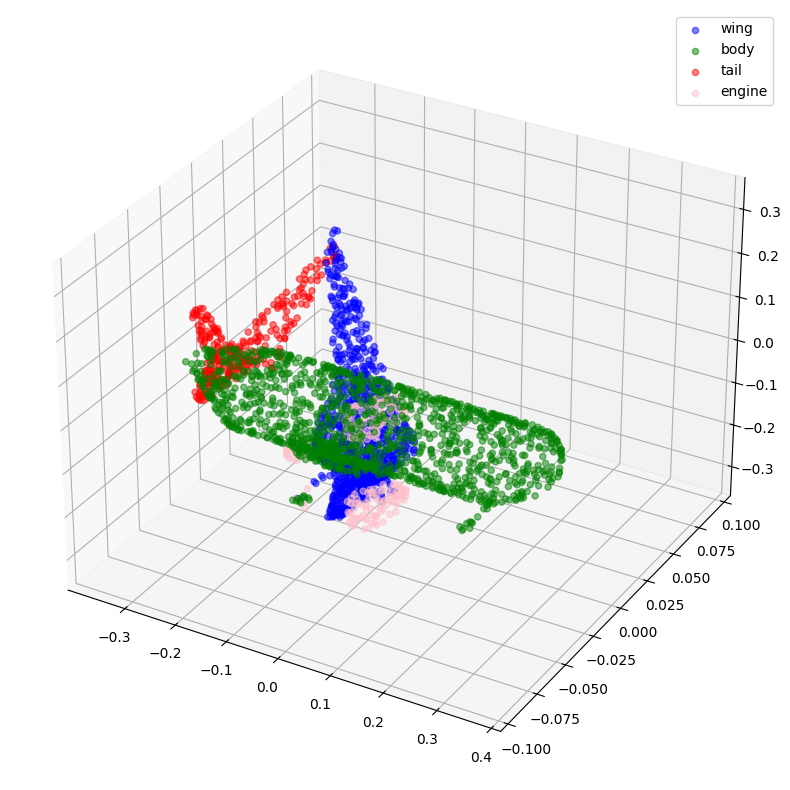
预处理
请注意，我们加载的所有点云都包含可变数量的点，这使得我们很难将它们批量处理。为了克服这个问题，我们从每个点云中随机采样固定数量的点。我们还对点云进行归一化，以使数据具有尺度不变性。
for index in tqdm(range(len(point_clouds))):
current_point_cloud = point_clouds[index]
current_label_cloud = point_cloud_labels[index]
current_labels = all_labels[index]
num_points = len(current_point_cloud)
# Randomly sampling respective indices.
sampled_indices = random.sample(list(range(num_points)), NUM_SAMPLE_POINTS)
# Sampling points corresponding to sampled indices.
sampled_point_cloud = np.array([current_point_cloud[i] for i in sampled_indices])
# Sampling corresponding one-hot encoded labels.
sampled_label_cloud = np.array([current_label_cloud[i] for i in sampled_indices])
# Sampling corresponding labels for visualization.
sampled_labels = np.array([current_labels[i] for i in sampled_indices])
# Normalizing sampled point cloud.
norm_point_cloud = sampled_point_cloud - np.mean(sampled_point_cloud, axis=0)
norm_point_cloud /= np.max(np.linalg.norm(norm_point_cloud, axis=1))
point_clouds[index] = norm_point_cloud
point_cloud_labels[index] = sampled_label_cloud
all_labels[index] = sampled_labels
100%|█████████████████████████████████████████████████████████████████████| 3694/3694 [00:08<00:00, 446.45it/s]
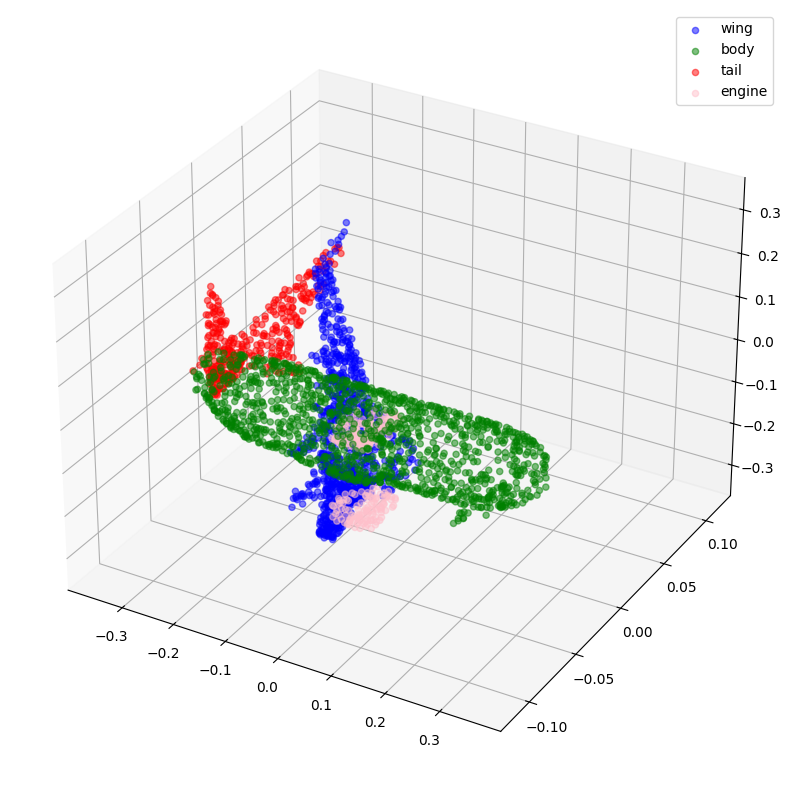
让我们可视化采样和归一化的点云及其相应的标签。
visualize_data(point_clouds[0], all_labels[0])
visualize_data(point_clouds[300], all_labels[300])
创建 TensorFlow 数据集
我们为训练和验证数据创建 tf.data.Dataset 对象。我们还通过对训练点云应用随机抖动来增强它们。
def load_data(point_cloud_batch, label_cloud_batch):
point_cloud_batch.set_shape([NUM_SAMPLE_POINTS, 3])
label_cloud_batch.set_shape([NUM_SAMPLE_POINTS, len(LABELS) + 1])
return point_cloud_batch, label_cloud_batch
def augment(point_cloud_batch, label_cloud_batch):
noise = tf.random.uniform(
tf.shape(label_cloud_batch), -0.001, 0.001, dtype=tf.float64
)
point_cloud_batch += noise[:, :, :3]
return point_cloud_batch, label_cloud_batch
def generate_dataset(point_clouds, label_clouds, is_training=True):
dataset = tf.data.Dataset.from_tensor_slices((point_clouds, label_clouds))
dataset = dataset.shuffle(BATCH_SIZE * 100) if is_training else dataset
dataset = dataset.map(load_data, num_parallel_calls=tf.data.AUTOTUNE)
dataset = dataset.batch(batch_size=BATCH_SIZE)
dataset = (
dataset.map(augment, num_parallel_calls=tf.data.AUTOTUNE)
if is_training
else dataset
)
return dataset
split_index = int(len(point_clouds) * (1 - VAL_SPLIT))
train_point_clouds = point_clouds[:split_index]
train_label_cloud = point_cloud_labels[:split_index]
total_training_examples = len(train_point_clouds)
val_point_clouds = point_clouds[split_index:]
val_label_cloud = point_cloud_labels[split_index:]
print("Num train point clouds:", len(train_point_clouds))
print("Num train point cloud labels:", len(train_label_cloud))
print("Num val point clouds:", len(val_point_clouds))
print("Num val point cloud labels:", len(val_label_cloud))
train_dataset = generate_dataset(train_point_clouds, train_label_cloud)
val_dataset = generate_dataset(val_point_clouds, val_label_cloud, is_training=False)
print("Train Dataset:", train_dataset)
print("Validation Dataset:", val_dataset)
Num train point clouds: 2955
Num train point cloud labels: 2955
Num val point clouds: 739
Num val point cloud labels: 739
Train Dataset: <_ParallelMapDataset element_spec=(TensorSpec(shape=(None, 1024, 3), dtype=tf.float64, name=None), TensorSpec(shape=(None, 1024, 5), dtype=tf.float64, name=None))>
Validation Dataset: <_BatchDataset element_spec=(TensorSpec(shape=(None, 1024, 3), dtype=tf.float64, name=None), TensorSpec(shape=(None, 1024, 5), dtype=tf.float64, name=None))>
PointNet 模型
下图描述了 PointNet 模型系列的内部结构
鉴于 PointNet 旨在将坐标的无序集合作为其输入数据，其架构需要匹配点云数据的以下特征属性
置换不变性
鉴于点云数据的非结构化性质，由 n 个点组成的扫描有 n! 种排列。后续的数据处理必须对不同的表示形式保持不变。为了使 PointNet 对输入排列保持不变，一旦将 n 个输入点映射到更高维空间，我们就会使用一个对称函数（例如最大池化）。结果是一个全局特征向量，旨在捕获 n 个输入点的聚合签名。全局特征向量与局部点特征一起用于分割。
变换不变性
如果物体经历某些变换，例如平移或缩放，分割输出应该保持不变。对于给定的输入点云，我们应用适当的刚性或仿射变换来实现姿态归一化。由于每个 n 个输入点都表示为一个向量，并且独立地映射到嵌入空间，因此应用几何变换只需将每个点与变换矩阵进行矩阵乘法即可。这受到空间变换网络概念的启发。
T-Net 的操作灵感来自于 PointNet 的更高级别架构。MLP（或全连接层）用于将输入点独立且相同地映射到更高维度的空间；最大池化用于编码全局特征向量，然后通过全连接层降低其维度。最后一个全连接层的输入相关特征然后与全局可训练的权重和偏置相结合，从而产生一个 3x3 的变换矩阵。
点交互
相邻点之间的交互通常携带有用的信息（即，不应孤立地处理单个点）。分类只需要利用全局特征，而分割必须能够利用局部点特征以及全局点特征。
注意：本节中提供的图来自原始论文。
现在我们了解了组成 PointNet 模型的部分，我们可以实现该模型。我们首先实现基本模块，即卷积块和多层感知机块。
def conv_block(x, filters, name):
x = layers.Conv1D(filters, kernel_size=1, padding="valid", name=f"{name}_conv")(x)
x = layers.BatchNormalization(name=f"{name}_batch_norm")(x)
return layers.Activation("relu", name=f"{name}_relu")(x)
def mlp_block(x, filters, name):
x = layers.Dense(filters, name=f"{name}_dense")(x)
x = layers.BatchNormalization(name=f"{name}_batch_norm")(x)
return layers.Activation("relu", name=f"{name}_relu")(x)
我们实现一个正则化器（取自这个例子）来强制特征空间中的正交性。 这是为了确保变换后的特征幅度不会变化太大。
class OrthogonalRegularizer(keras.regularizers.Regularizer):
"""Reference: https://keras.org.cn/examples/vision/pointnet/#build-a-model"""
def __init__(self, num_features, l2reg=0.001):
self.num_features = num_features
self.l2reg = l2reg
self.identity = keras.ops.eye(num_features)
def __call__(self, x):
x = keras.ops.reshape(x, (-1, self.num_features, self.num_features))
xxt = keras.ops.tensordot(x, x, axes=(2, 2))
xxt = keras.ops.reshape(xxt, (-1, self.num_features, self.num_features))
return keras.ops.sum(self.l2reg * keras.ops.square(xxt - self.identity))
def get_config(self):
config = super().get_config()
config.update({"num_features": self.num_features, "l2reg_strength": self.l2reg})
return config
下一个部分是变换网络，我们之前已经解释过。
def transformation_net(inputs, num_features, name):
"""
Reference: https://keras.org.cn/examples/vision/pointnet/#build-a-model.
The `filters` values come from the original paper:
https://arxiv.org/abs/1612.00593.
"""
x = conv_block(inputs, filters=64, name=f"{name}_1")
x = conv_block(x, filters=128, name=f"{name}_2")
x = conv_block(x, filters=1024, name=f"{name}_3")
x = layers.GlobalMaxPooling1D()(x)
x = mlp_block(x, filters=512, name=f"{name}_1_1")
x = mlp_block(x, filters=256, name=f"{name}_2_1")
return layers.Dense(
num_features * num_features,
kernel_initializer="zeros",
bias_initializer=keras.initializers.Constant(np.eye(num_features).flatten()),
activity_regularizer=OrthogonalRegularizer(num_features),
name=f"{name}_final",
)(x)
def transformation_block(inputs, num_features, name):
transformed_features = transformation_net(inputs, num_features, name=name)
transformed_features = layers.Reshape((num_features, num_features))(
transformed_features
)
return layers.Dot(axes=(2, 1), name=f"{name}_mm")([inputs, transformed_features])
最后，我们将上述模块组合在一起，实现分割模型。
def get_shape_segmentation_model(num_points, num_classes):
input_points = keras.Input(shape=(None, 3))
# PointNet Classification Network.
transformed_inputs = transformation_block(
input_points, num_features=3, name="input_transformation_block"
)
features_64 = conv_block(transformed_inputs, filters=64, name="features_64")
features_128_1 = conv_block(features_64, filters=128, name="features_128_1")
features_128_2 = conv_block(features_128_1, filters=128, name="features_128_2")
transformed_features = transformation_block(
features_128_2, num_features=128, name="transformed_features"
)
features_512 = conv_block(transformed_features, filters=512, name="features_512")
features_2048 = conv_block(features_512, filters=2048, name="pre_maxpool_block")
global_features = layers.MaxPool1D(pool_size=num_points, name="global_features")(
features_2048
)
global_features = keras.ops.tile(global_features, [1, num_points, 1])
# Segmentation head.
segmentation_input = layers.Concatenate(name="segmentation_input")(
[
features_64,
features_128_1,
features_128_2,
transformed_features,
features_512,
global_features,
]
)
segmentation_features = conv_block(
segmentation_input, filters=128, name="segmentation_features"
)
outputs = layers.Conv1D(
num_classes, kernel_size=1, activation="softmax", name="segmentation_head"
)(segmentation_features)
return keras.Model(input_points, outputs)
实例化模型
x, y = next(iter(train_dataset))
num_points = x.shape[1]
num_classes = y.shape[-1]
segmentation_model = get_shape_segmentation_model(num_points, num_classes)
segmentation_model.summary()
Model: "functional_1"
┏━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━┳━━━━━━━━━━━━━━━━━━━━━━┓ ┃ Layer (type) ┃ Output Shape ┃ Param # ┃ Connected to ┃ ┡━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━╇━━━━━━━━━━━━━━━━━━━━━━┩ │ input_layer │ (None, None, 3) │ 0 │ - │ │ (InputLayer) │ │ │ │ ├─────────────────────┼───────────────────┼─────────┼──────────────────────┤ │ input_transformati… │ (None, None, 64) │ 256 │ input_layer[0][0] │ │ (Conv1D) │ │ │ │ ├─────────────────────┼───────────────────┼─────────┼──────────────────────┤ │ input_transformati… │ (None, None, 64) │ 256 │ input_transformatio… │ │ (BatchNormalizatio… │ │ │ │ ├─────────────────────┼───────────────────┼─────────┼──────────────────────┤ │ input_transformati… │ (None, None, 64) │ 0 │ input_transformatio… │ │ (Activation) │ │ │ │ ├─────────────────────┼───────────────────┼─────────┼──────────────────────┤ │ input_transformati… │ (None, None, 128) │ 8,320 │ input_transformatio… │ │ (Conv1D) │ │ │ │ ├─────────────────────┼───────────────────┼─────────┼──────────────────────┤ │ input_transformati… │ (None, None, 128) │ 512 │ input_transformatio… │ │ (BatchNormalizatio… │ │ │ │ ├─────────────────────┼───────────────────┼─────────┼──────────────────────┤ │ input_transformati… │ (None, None, 128) │ 0 │ input_transformatio… │ │ (Activation) │ │ │ │ ├─────────────────────┼───────────────────┼─────────┼──────────────────────┤ │ input_transformati… │ (None, None, │ 132,096 │ input_transformatio… │ │ (Conv1D) │ 1024) │ │ │ ├─────────────────────┼───────────────────┼─────────┼──────────────────────┤ │ input_transformati… │ (None, None, │ 4,096 │ input_transformatio… │ │ (BatchNormalizatio… │ 1024) │ │ │ ├─────────────────────┼───────────────────┼─────────┼──────────────────────┤ │ input_transformati… │ (None, None, │ 0 │ input_transformatio… │ │ (Activation) │ 1024) │ │ │ ├─────────────────────┼───────────────────┼─────────┼──────────────────────┤ │ global_max_pooling… │ (None, 1024) │ 0 │ input_transformatio… │ │ (GlobalMaxPooling1… │ │ │ │ ├─────────────────────┼───────────────────┼─────────┼──────────────────────┤ │ input_transformati… │ (None, 512) │ 524,800 │ global_max_pooling1… │ │ (Dense) │ │ │ │ ├─────────────────────┼───────────────────┼─────────┼──────────────────────┤ │ input_transformati… │ (None, 512) │ 2,048 │ input_transformatio… │ │ (BatchNormalizatio… │ │ │ │ ├─────────────────────┼───────────────────┼─────────┼──────────────────────┤ │ input_transformati… │ (None, 512) │ 0 │ input_transformatio… │ │ (Activation) │ │ │ │ ├─────────────────────┼───────────────────┼─────────┼──────────────────────┤ │ input_transformati… │ (None, 256) │ 131,328 │ input_transformatio… │ │ (Dense) │ │ │ │ ├─────────────────────┼───────────────────┼─────────┼──────────────────────┤ │ input_transformati… │ (None, 256) │ 1,024 │ input_transformatio… │ │ (BatchNormalizatio… │ │ │ │ ├─────────────────────┼───────────────────┼─────────┼──────────────────────┤ │ input_transformati… │ (None, 256) │ 0 │ input_transformatio… │ │ (Activation) │ │ │ │ ├─────────────────────┼───────────────────┼─────────┼──────────────────────┤ │ input_transformati… │ (None, 9) │ 2,313 │ input_transformatio… │ │ (Dense) │ │ │ │ ├─────────────────────┼───────────────────┼─────────┼──────────────────────┤ │ reshape (Reshape) │ (None, 3, 3) │ 0 │ input_transformatio… │ ├─────────────────────┼───────────────────┼─────────┼──────────────────────┤ │ input_transformati… │ (None, None, 3) │ 0 │ input_layer[0][0], │ │ (Dot) │ │ │ reshape[0][0] │ ├─────────────────────┼───────────────────┼─────────┼──────────────────────┤ │ features_64_conv │ (None, None, 64) │ 256 │ input_transformatio… │ │ (Conv1D) │ │ │ │ ├─────────────────────┼───────────────────┼─────────┼──────────────────────┤ │ features_64_batch_… │ (None, None, 64) │ 256 │ features_64_conv[0]… │ │ (BatchNormalizatio… │ │ │ │ ├─────────────────────┼───────────────────┼─────────┼──────────────────────┤ │ features_64_relu │ (None, None, 64) │ 0 │ features_64_batch_n… │ │ (Activation) │ │ │ │ ├─────────────────────┼───────────────────┼─────────┼──────────────────────┤ │ features_128_1_conv │ (None, None, 128) │ 8,320 │ features_64_relu[0]… │ │ (Conv1D) │ │ │ │ ├─────────────────────┼───────────────────┼─────────┼──────────────────────┤ │ features_128_1_bat… │ (None, None, 128) │ 512 │ features_128_1_conv… │ │ (BatchNormalizatio… │ │ │ │ ├─────────────────────┼───────────────────┼─────────┼──────────────────────┤ │ features_128_1_relu │ (None, None, 128) │ 0 │ features_128_1_batc… │ │ (Activation) │ │ │ │ ├─────────────────────┼───────────────────┼─────────┼──────────────────────┤ │ features_128_2_conv │ (None, None, 128) │ 16,512 │ features_128_1_relu… │ │ (Conv1D) │ │ │ │ ├─────────────────────┼───────────────────┼─────────┼──────────────────────┤ │ features_128_2_bat… │ (None, None, 128) │ 512 │ features_128_2_conv… │ │ (BatchNormalizatio… │ │ │ │ ├─────────────────────┼───────────────────┼─────────┼──────────────────────┤ │ features_128_2_relu │ (None, None, 128) │ 0 │ features_128_2_batc… │ │ (Activation) │ │ │ │ ├─────────────────────┼───────────────────┼─────────┼──────────────────────┤ │ transformed_featur… │ (None, None, 64) │ 8,256 │ features_128_2_relu… │ │ (Conv1D) │ │ │ │ ├─────────────────────┼───────────────────┼─────────┼──────────────────────┤ │ transformed_featur… │ (None, None, 64) │ 256 │ transformed_feature… │ │ (BatchNormalizatio… │ │ │ │ ├─────────────────────┼───────────────────┼─────────┼──────────────────────┤ │ transformed_featur… │ (None, None, 64) │ 0 │ transformed_feature… │ │ (Activation) │ │ │ │ ├─────────────────────┼───────────────────┼─────────┼──────────────────────┤ │ transformed_featur… │ (None, None, 128) │ 8,320 │ transformed_feature… │ │ (Conv1D) │ │ │ │ ├─────────────────────┼───────────────────┼─────────┼──────────────────────┤ │ transformed_featur… │ (None, None, 128) │ 512 │ transformed_feature… │ │ (BatchNormalizatio… │ │ │ │ ├─────────────────────┼───────────────────┼─────────┼──────────────────────┤ │ transformed_featur… │ (None, None, 128) │ 0 │ transformed_feature… │ │ (Activation) │ │ │ │ ├─────────────────────┼───────────────────┼─────────┼──────────────────────┤ │ transformed_featur… │ (None, None, │ 132,096 │ transformed_feature… │ │ (Conv1D) │ 1024) │ │ │ ├─────────────────────┼───────────────────┼─────────┼──────────────────────┤ │ transformed_featur… │ (None, None, │ 4,096 │ transformed_feature… │ │ (BatchNormalizatio… │ 1024) │ │ │ ├─────────────────────┼───────────────────┼─────────┼──────────────────────┤ │ transformed_featur… │ (None, None, │ 0 │ transformed_feature… │ │ (Activation) │ 1024) │ │ │ ├─────────────────────┼───────────────────┼─────────┼──────────────────────┤ │ global_max_pooling… │ (None, 1024) │ 0 │ transformed_feature… │ │ (GlobalMaxPooling1… │ │ │ │ ├─────────────────────┼───────────────────┼─────────┼──────────────────────┤ │ transformed_featur… │ (None, 512) │ 524,800 │ global_max_pooling1… │ │ (Dense) │ │ │ │ ├─────────────────────┼───────────────────┼─────────┼──────────────────────┤ │ transformed_featur… │ (None, 512) │ 2,048 │ transformed_feature… │ │ (BatchNormalizatio… │ │ │ │ ├─────────────────────┼───────────────────┼─────────┼──────────────────────┤ │ transformed_featur… │ (None, 512) │ 0 │ transformed_feature… │ │ (Activation) │ │ │ │ ├─────────────────────┼───────────────────┼─────────┼──────────────────────┤ │ transformed_featur… │ (None, 256) │ 131,328 │ transformed_feature… │ │ (Dense) │ │ │ │ ├─────────────────────┼───────────────────┼─────────┼──────────────────────┤ │ transformed_featur… │ (None, 256) │ 1,024 │ transformed_feature… │ │ (BatchNormalizatio… │ │ │ │ ├─────────────────────┼───────────────────┼─────────┼──────────────────────┤ │ transformed_featur… │ (None, 256) │ 0 │ transformed_feature… │ │ (Activation) │ │ │ │ ├─────────────────────┼───────────────────┼─────────┼──────────────────────┤ │ transformed_featur… │ (None, 16384) │ 4,210,… │ transformed_feature… │ │ (Dense) │ │ │ │ ├─────────────────────┼───────────────────┼─────────┼──────────────────────┤ │ reshape_1 (Reshape) │ (None, 128, 128) │ 0 │ transformed_feature… │ ├─────────────────────┼───────────────────┼─────────┼──────────────────────┤ │ transformed_featur… │ (None, None, 128) │ 0 │ features_128_2_relu… │ │ (Dot) │ │ │ reshape_1[0][0] │ ├─────────────────────┼───────────────────┼─────────┼──────────────────────┤ │ features_512_conv │ (None, None, 512) │ 66,048 │ transformed_feature… │ │ (Conv1D) │ │ │ │ ├─────────────────────┼───────────────────┼─────────┼──────────────────────┤ │ features_512_batch… │ (None, None, 512) │ 2,048 │ features_512_conv[0… │ │ (BatchNormalizatio… │ │ │ │ ├─────────────────────┼───────────────────┼─────────┼──────────────────────┤ │ features_512_relu │ (None, None, 512) │ 0 │ features_512_batch_… │ │ (Activation) │ │ │ │ ├─────────────────────┼───────────────────┼─────────┼──────────────────────┤ │ pre_maxpool_block_… │ (None, None, │ 1,050,… │ features_512_relu[0… │ │ (Conv1D) │ 2048) │ │ │ ├─────────────────────┼───────────────────┼─────────┼──────────────────────┤ │ pre_maxpool_block_… │ (None, None, │ 8,192 │ pre_maxpool_block_c… │ │ (BatchNormalizatio… │ 2048) │ │ │ ├─────────────────────┼───────────────────┼─────────┼──────────────────────┤ │ pre_maxpool_block_… │ (None, None, │ 0 │ pre_maxpool_block_b… │ │ (Activation) │ 2048) │ │ │ ├─────────────────────┼───────────────────┼─────────┼──────────────────────┤ │ global_features │ (None, None, │ 0 │ pre_maxpool_block_r… │ │ (MaxPooling1D) │ 2048) │ │ │ ├─────────────────────┼───────────────────┼─────────┼──────────────────────┤ │ tile (Tile) │ (None, None, │ 0 │ global_features[0][… │ │ │ 2048) │ │ │ ├─────────────────────┼───────────────────┼─────────┼──────────────────────┤ │ segmentation_input │ (None, None, │ 0 │ features_64_relu[0]… │ │ (Concatenate) │ 3008) │ │ features_128_1_relu… │ │ │ │ │ features_128_2_relu… │ │ │ │ │ transformed_feature… │ │ │ │ │ features_512_relu[0… │ │ │ │ │ tile[0][0] │ ├─────────────────────┼───────────────────┼─────────┼──────────────────────┤ │ segmentation_featu… │ (None, None, 128) │ 385,152 │ segmentation_input[… │ │ (Conv1D) │ │ │ │ ├─────────────────────┼───────────────────┼─────────┼──────────────────────┤ │ segmentation_featu… │ (None, None, 128) │ 512 │ segmentation_featur… │ │ (BatchNormalizatio… │ │ │ │ ├─────────────────────┼───────────────────┼─────────┼──────────────────────┤ │ segmentation_featu… │ (None, None, 128) │ 0 │ segmentation_featur… │ │ (Activation) │ │ │ │ ├─────────────────────┼───────────────────┼─────────┼──────────────────────┤ │ segmentation_head │ (None, None, 5) │ 645 │ segmentation_featur… │ │ (Conv1D) │ │ │ │ └─────────────────────┴───────────────────┴─────────┴──────────────────────┘
Total params: 7,370,062 (28.11 MB)
Trainable params: 7,356,110 (28.06 MB)
Non-trainable params: 13,952 (54.50 KB)
训练
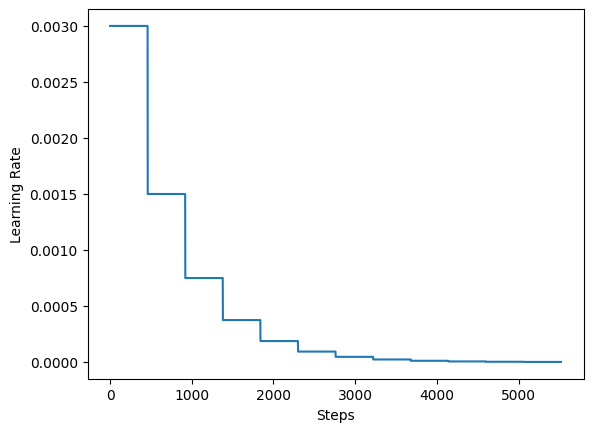
对于训练，作者建议使用学习率调度，该调度每 20 个 epoch 将初始学习率减半。在本示例中，我们使用 5 个 epoch。
steps_per_epoch = total_training_examples // BATCH_SIZE
total_training_steps = steps_per_epoch * EPOCHS
print(f"Steps per epoch: {steps_per_epoch}.")
print(f"Total training steps: {total_training_steps}.")
lr_schedule = keras.optimizers.schedules.ExponentialDecay(
initial_learning_rate=0.003,
decay_steps=steps_per_epoch * 5,
decay_rate=0.5,
staircase=True,
)
steps = range(total_training_steps)
lrs = [lr_schedule(step) for step in steps]
plt.plot(lrs)
plt.xlabel("Steps")
plt.ylabel("Learning Rate")
plt.show()
Steps per epoch: 92.
Total training steps: 5520.
最后，我们实现一个用于运行实验并启动模型训练的实用程序。
def run_experiment(epochs):
segmentation_model = get_shape_segmentation_model(num_points, num_classes)
segmentation_model.compile(
optimizer=keras.optimizers.Adam(learning_rate=lr_schedule),
loss=keras.losses.CategoricalCrossentropy(),
metrics=["accuracy"],
)
checkpoint_filepath = "checkpoint.weights.h5"
checkpoint_callback = keras.callbacks.ModelCheckpoint(
checkpoint_filepath,
monitor="val_loss",
save_best_only=True,
save_weights_only=True,
)
history = segmentation_model.fit(
train_dataset,
validation_data=val_dataset,
epochs=epochs,
callbacks=[checkpoint_callback],
)
segmentation_model.load_weights(checkpoint_filepath)
return segmentation_model, history
segmentation_model, history = run_experiment(epochs=EPOCHS)
Epoch 1/60
2/93 [37m━━━━━━━━━━━━━━━━━━━━ 7s 86ms/step - accuracy: 0.1427 - loss: 48748.8203
WARNING: All log messages before absl::InitializeLog() is called are written to STDERR
I0000 00:00:1699916678.434176 90326 device_compiler.h:187] Compiled cluster using XLA! This line is logged at most once for the lifetime of the process.
93/93 ━━━━━━━━━━━━━━━━━━━━ 53s 259ms/step - accuracy: 0.3739 - loss: 27980.7305 - val_accuracy: 0.4340 - val_loss: 10361231.0000
Epoch 2/60
93/93 ━━━━━━━━━━━━━━━━━━━━ 48s 82ms/step - accuracy: 0.6355 - loss: 339.9151 - val_accuracy: 0.3820 - val_loss: 19069320.0000
Epoch 3/60
93/93 ━━━━━━━━━━━━━━━━━━━━ 8s 82ms/step - accuracy: 0.6695 - loss: 281.5728 - val_accuracy: 0.2859 - val_loss: 15993839.0000
Epoch 4/60
93/93 ━━━━━━━━━━━━━━━━━━━━ 8s 89ms/step - accuracy: 0.6812 - loss: 253.0939 - val_accuracy: 0.2287 - val_loss: 9633191.0000
Epoch 5/60
93/93 ━━━━━━━━━━━━━━━━━━━━ 8s 89ms/step - accuracy: 0.6873 - loss: 231.1317 - val_accuracy: 0.3030 - val_loss: 6001454.0000
Epoch 6/60
93/93 ━━━━━━━━━━━━━━━━━━━━ 8s 88ms/step - accuracy: 0.6860 - loss: 216.6793 - val_accuracy: 0.0620 - val_loss: 1945100.8750
Epoch 7/60
93/93 ━━━━━━━━━━━━━━━━━━━━ 8s 82ms/step - accuracy: 0.6947 - loss: 210.2683 - val_accuracy: 0.4539 - val_loss: 7908162.5000
Epoch 8/60
93/93 ━━━━━━━━━━━━━━━━━━━━ 8s 82ms/step - accuracy: 0.7014 - loss: 203.2560 - val_accuracy: 0.4035 - val_loss: 17741164.0000
Epoch 9/60
93/93 ━━━━━━━━━━━━━━━━━━━━ 8s 82ms/step - accuracy: 0.7006 - loss: 197.3710 - val_accuracy: 0.1900 - val_loss: 34120616.0000
Epoch 10/60
93/93 ━━━━━━━━━━━━━━━━━━━━ 8s 82ms/step - accuracy: 0.7047 - loss: 192.0777 - val_accuracy: 0.3391 - val_loss: 33157422.0000
Epoch 11/60
93/93 ━━━━━━━━━━━━━━━━━━━━ 8s 82ms/step - accuracy: 0.7102 - loss: 188.4875 - val_accuracy: 0.3394 - val_loss: 4630613.5000
Epoch 12/60
93/93 ━━━━━━━━━━━━━━━━━━━━ 8s 89ms/step - accuracy: 0.7186 - loss: 184.9940 - val_accuracy: 0.1662 - val_loss: 487790.1250
Epoch 13/60
93/93 ━━━━━━━━━━━━━━━━━━━━ 8s 89ms/step - accuracy: 0.7175 - loss: 182.7206 - val_accuracy: 0.1602 - val_loss: 70590.3203
Epoch 14/60
93/93 ━━━━━━━━━━━━━━━━━━━━ 8s 88ms/step - accuracy: 0.7159 - loss: 180.5028 - val_accuracy: 0.1631 - val_loss: 16990.2324
Epoch 15/60
93/93 ━━━━━━━━━━━━━━━━━━━━ 8s 88ms/step - accuracy: 0.7201 - loss: 180.1674 - val_accuracy: 0.2318 - val_loss: 4992.7783
Epoch 16/60
93/93 ━━━━━━━━━━━━━━━━━━━━ 8s 88ms/step - accuracy: 0.7222 - loss: 176.5523 - val_accuracy: 0.6246 - val_loss: 647.5634
Epoch 17/60
93/93 ━━━━━━━━━━━━━━━━━━━━ 8s 88ms/step - accuracy: 0.7291 - loss: 175.6139 - val_accuracy: 0.6551 - val_loss: 324.0956
Epoch 18/60
93/93 ━━━━━━━━━━━━━━━━━━━━ 8s 88ms/step - accuracy: 0.7285 - loss: 175.0228 - val_accuracy: 0.6430 - val_loss: 257.9340
Epoch 19/60
93/93 ━━━━━━━━━━━━━━━━━━━━ 8s 88ms/step - accuracy: 0.7300 - loss: 172.7668 - val_accuracy: 0.6399 - val_loss: 253.2745
Epoch 20/60
93/93 ━━━━━━━━━━━━━━━━━━━━ 8s 89ms/step - accuracy: 0.7316 - loss: 172.9001 - val_accuracy: 0.6084 - val_loss: 232.9293
Epoch 21/60
93/93 ━━━━━━━━━━━━━━━━━━━━ 8s 89ms/step - accuracy: 0.7364 - loss: 170.8767 - val_accuracy: 0.6451 - val_loss: 191.7183
Epoch 22/60
93/93 ━━━━━━━━━━━━━━━━━━━━ 8s 88ms/step - accuracy: 0.7395 - loss: 171.4525 - val_accuracy: 0.6825 - val_loss: 180.2473
Epoch 23/60
93/93 ━━━━━━━━━━━━━━━━━━━━ 8s 82ms/step - accuracy: 0.7392 - loss: 170.1975 - val_accuracy: 0.6095 - val_loss: 180.3243
Epoch 24/60
93/93 ━━━━━━━━━━━━━━━━━━━━ 8s 88ms/step - accuracy: 0.7362 - loss: 169.2144 - val_accuracy: 0.6017 - val_loss: 178.3013
Epoch 25/60
93/93 ━━━━━━━━━━━━━━━━━━━━ 8s 82ms/step - accuracy: 0.7409 - loss: 169.2571 - val_accuracy: 0.6582 - val_loss: 178.3481
Epoch 26/60
93/93 ━━━━━━━━━━━━━━━━━━━━ 8s 89ms/step - accuracy: 0.7415 - loss: 167.7480 - val_accuracy: 0.6808 - val_loss: 177.8774
Epoch 27/60
93/93 ━━━━━━━━━━━━━━━━━━━━ 8s 89ms/step - accuracy: 0.7440 - loss: 167.7844 - val_accuracy: 0.7131 - val_loss: 176.5841
Epoch 28/60
93/93 ━━━━━━━━━━━━━━━━━━━━ 8s 88ms/step - accuracy: 0.7423 - loss: 167.5307 - val_accuracy: 0.6891 - val_loss: 176.1687
Epoch 29/60
93/93 ━━━━━━━━━━━━━━━━━━━━ 8s 88ms/step - accuracy: 0.7409 - loss: 166.4581 - val_accuracy: 0.7136 - val_loss: 174.9417
Epoch 30/60
93/93 ━━━━━━━━━━━━━━━━━━━━ 8s 88ms/step - accuracy: 0.7419 - loss: 165.9243 - val_accuracy: 0.7407 - val_loss: 173.0663
Epoch 31/60
93/93 ━━━━━━━━━━━━━━━━━━━━ 8s 88ms/step - accuracy: 0.7471 - loss: 166.9746 - val_accuracy: 0.7454 - val_loss: 172.9663
Epoch 32/60
93/93 ━━━━━━━━━━━━━━━━━━━━ 8s 82ms/step - accuracy: 0.7472 - loss: 165.9707 - val_accuracy: 0.7480 - val_loss: 173.9868
Epoch 33/60
93/93 ━━━━━━━━━━━━━━━━━━━━ 8s 82ms/step - accuracy: 0.7443 - loss: 165.9368 - val_accuracy: 0.7076 - val_loss: 174.4526
Epoch 34/60
93/93 ━━━━━━━━━━━━━━━━━━━━ 8s 82ms/step - accuracy: 0.7496 - loss: 165.5322 - val_accuracy: 0.7441 - val_loss: 174.6099
Epoch 35/60
93/93 ━━━━━━━━━━━━━━━━━━━━ 8s 82ms/step - accuracy: 0.7453 - loss: 164.2007 - val_accuracy: 0.7469 - val_loss: 174.2793
Epoch 36/60
93/93 ━━━━━━━━━━━━━━━━━━━━ 8s 82ms/step - accuracy: 0.7503 - loss: 165.3418 - val_accuracy: 0.7469 - val_loss: 174.0812
Epoch 37/60
93/93 ━━━━━━━━━━━━━━━━━━━━ 8s 82ms/step - accuracy: 0.7491 - loss: 164.4796 - val_accuracy: 0.7524 - val_loss: 173.9656
Epoch 38/60
93/93 ━━━━━━━━━━━━━━━━━━━━ 10s 82ms/step - accuracy: 0.7489 - loss: 164.4573 - val_accuracy: 0.7516 - val_loss: 175.3401
Epoch 39/60
93/93 ━━━━━━━━━━━━━━━━━━━━ 8s 82ms/step - accuracy: 0.7437 - loss: 163.4484 - val_accuracy: 0.7532 - val_loss: 173.8172
Epoch 40/60
93/93 ━━━━━━━━━━━━━━━━━━━━ 8s 82ms/step - accuracy: 0.7507 - loss: 163.6720 - val_accuracy: 0.7537 - val_loss: 173.9127
Epoch 41/60
93/93 ━━━━━━━━━━━━━━━━━━━━ 8s 82ms/step - accuracy: 0.7506 - loss: 164.0555 - val_accuracy: 0.7556 - val_loss: 173.0979
Epoch 42/60
93/93 ━━━━━━━━━━━━━━━━━━━━ 8s 89ms/step - accuracy: 0.7517 - loss: 164.1554 - val_accuracy: 0.7562 - val_loss: 172.8895
Epoch 43/60
93/93 ━━━━━━━━━━━━━━━━━━━━ 10s 82ms/step - accuracy: 0.7527 - loss: 164.6351 - val_accuracy: 0.7567 - val_loss: 173.0476
Epoch 44/60
93/93 ━━━━━━━━━━━━━━━━━━━━ 8s 88ms/step - accuracy: 0.7505 - loss: 164.1568 - val_accuracy: 0.7571 - val_loss: 172.2751
Epoch 45/60
93/93 ━━━━━━━━━━━━━━━━━━━━ 8s 88ms/step - accuracy: 0.7500 - loss: 163.8129 - val_accuracy: 0.7579 - val_loss: 171.8897
Epoch 46/60
93/93 ━━━━━━━━━━━━━━━━━━━━ 8s 82ms/step - accuracy: 0.7534 - loss: 163.6473 - val_accuracy: 0.7577 - val_loss: 172.5457
Epoch 47/60
93/93 ━━━━━━━━━━━━━━━━━━━━ 8s 82ms/step - accuracy: 0.7510 - loss: 163.7318 - val_accuracy: 0.7580 - val_loss: 172.2256
Epoch 48/60
93/93 ━━━━━━━━━━━━━━━━━━━━ 8s 82ms/step - accuracy: 0.7517 - loss: 163.3274 - val_accuracy: 0.7575 - val_loss: 172.3276
Epoch 49/60
93/93 ━━━━━━━━━━━━━━━━━━━━ 8s 89ms/step - accuracy: 0.7511 - loss: 163.5069 - val_accuracy: 0.7581 - val_loss: 171.2155
Epoch 50/60
93/93 ━━━━━━━━━━━━━━━━━━━━ 8s 89ms/step - accuracy: 0.7507 - loss: 163.7366 - val_accuracy: 0.7578 - val_loss: 171.1100
Epoch 51/60
93/93 ━━━━━━━━━━━━━━━━━━━━ 8s 82ms/step - accuracy: 0.7519 - loss: 163.1190 - val_accuracy: 0.7580 - val_loss: 171.7971
Epoch 52/60
93/93 ━━━━━━━━━━━━━━━━━━━━ 8s 81ms/step - accuracy: 0.7510 - loss: 162.7351 - val_accuracy: 0.7579 - val_loss: 171.9780
Epoch 53/60
93/93 ━━━━━━━━━━━━━━━━━━━━ 8s 82ms/step - accuracy: 0.7510 - loss: 162.9639 - val_accuracy: 0.7577 - val_loss: 171.6770
Epoch 54/60
93/93 ━━━━━━━━━━━━━━━━━━━━ 8s 88ms/step - accuracy: 0.7530 - loss: 162.7419 - val_accuracy: 0.7578 - val_loss: 170.5556
Epoch 55/60
93/93 ━━━━━━━━━━━━━━━━━━━━ 8s 82ms/step - accuracy: 0.7515 - loss: 163.2893 - val_accuracy: 0.7582 - val_loss: 171.9172
Epoch 56/60
93/93 ━━━━━━━━━━━━━━━━━━━━ 8s 82ms/step - accuracy: 0.7505 - loss: 164.2843 - val_accuracy: 0.7584 - val_loss: 171.9182
Epoch 57/60
93/93 ━━━━━━━━━━━━━━━━━━━━ 8s 82ms/step - accuracy: 0.7498 - loss: 162.6679 - val_accuracy: 0.7587 - val_loss: 173.7610
Epoch 58/60
93/93 ━━━━━━━━━━━━━━━━━━━━ 8s 82ms/step - accuracy: 0.7523 - loss: 163.3332 - val_accuracy: 0.7585 - val_loss: 172.5207
Epoch 59/60
93/93 ━━━━━━━━━━━━━━━━━━━━ 8s 82ms/step - accuracy: 0.7529 - loss: 162.4575 - val_accuracy: 0.7586 - val_loss: 171.6861
Epoch 60/60
93/93 ━━━━━━━━━━━━━━━━━━━━ 8s 82ms/step - accuracy: 0.7498 - loss: 162.9523 - val_accuracy: 0.7586 - val_loss: 172.3012
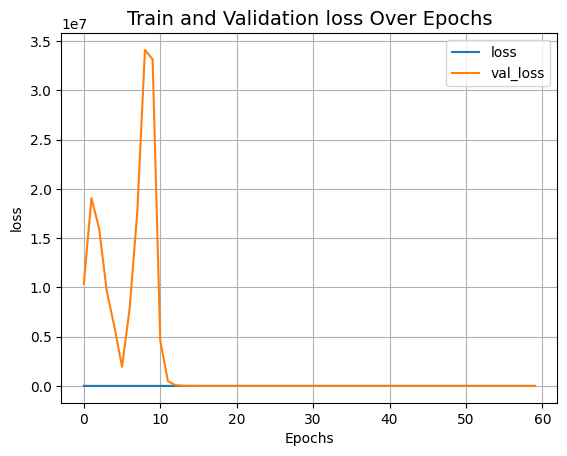
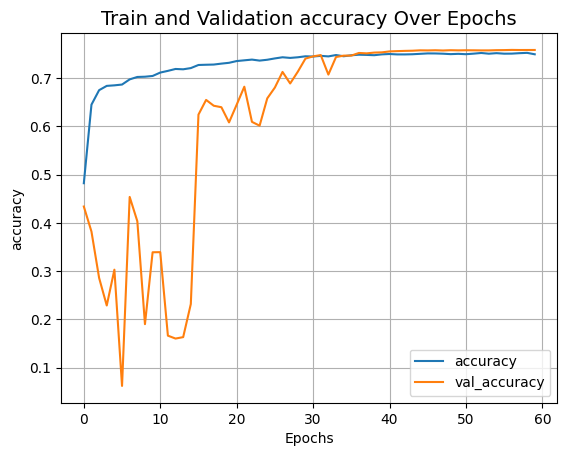
可视化训练过程
def plot_result(item):
plt.plot(history.history[item], label=item)
plt.plot(history.history["val_" + item], label="val_" + item)
plt.xlabel("Epochs")
plt.ylabel(item)
plt.title("Train and Validation {} Over Epochs".format(item), fontsize=14)
plt.legend()
plt.grid()
plt.show()
plot_result("loss")
plot_result("accuracy")
推理
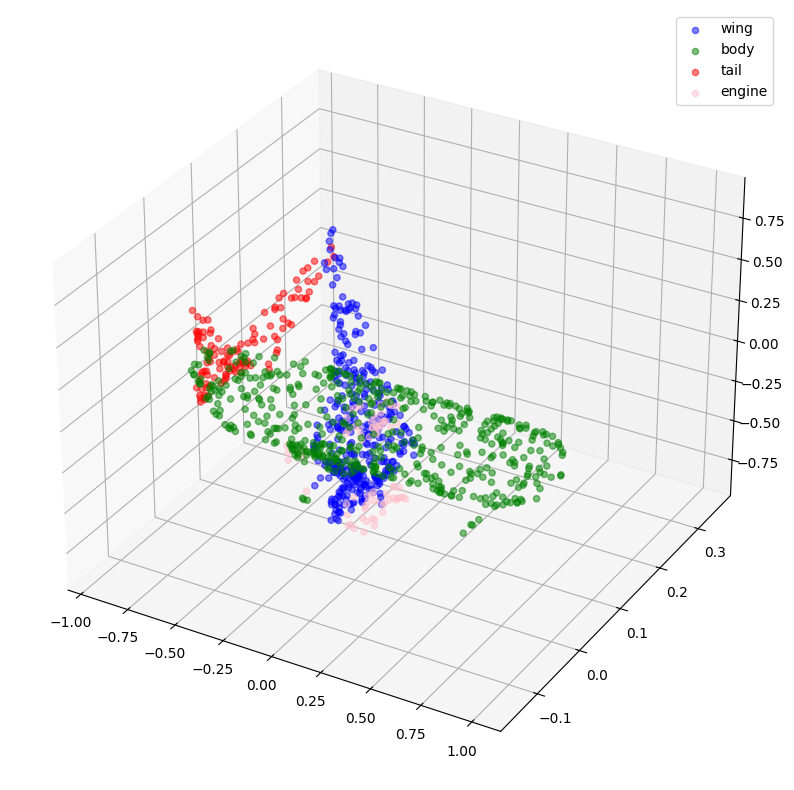
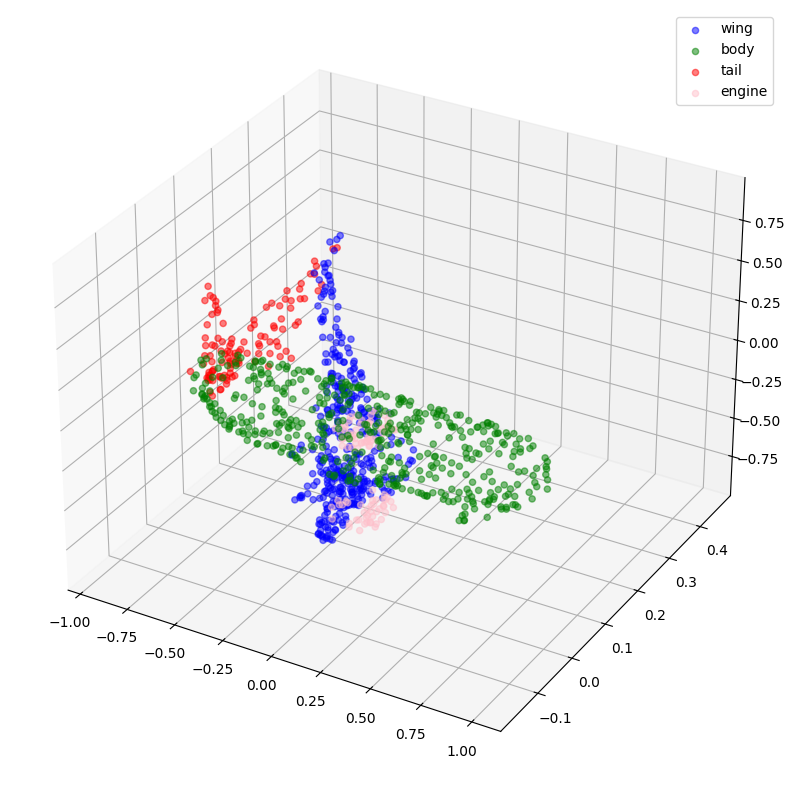
validation_batch = next(iter(val_dataset))
val_predictions = segmentation_model.predict(validation_batch[0])
print(f"Validation prediction shape: {val_predictions.shape}")
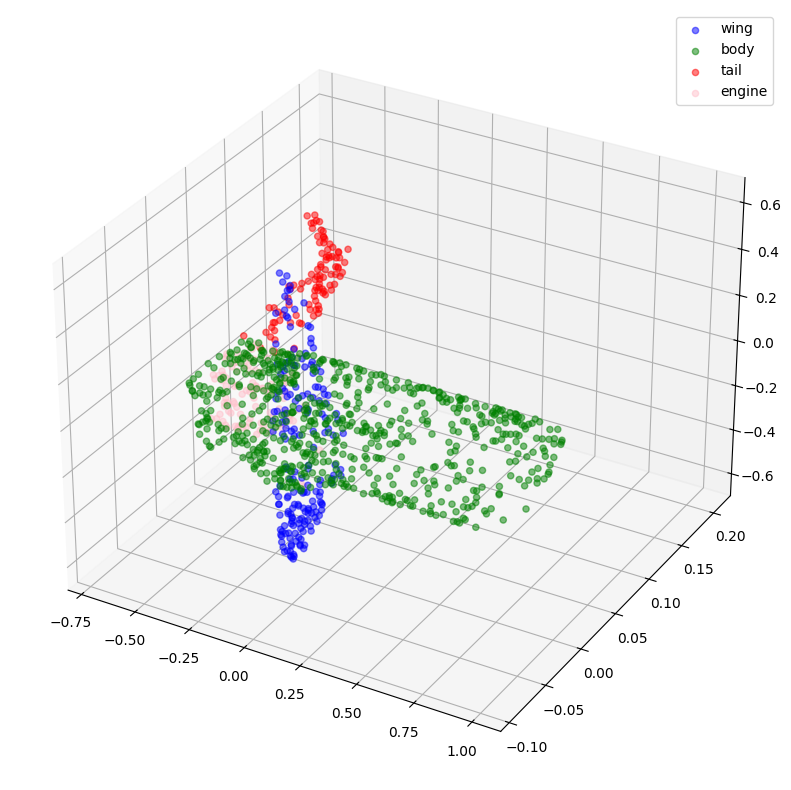
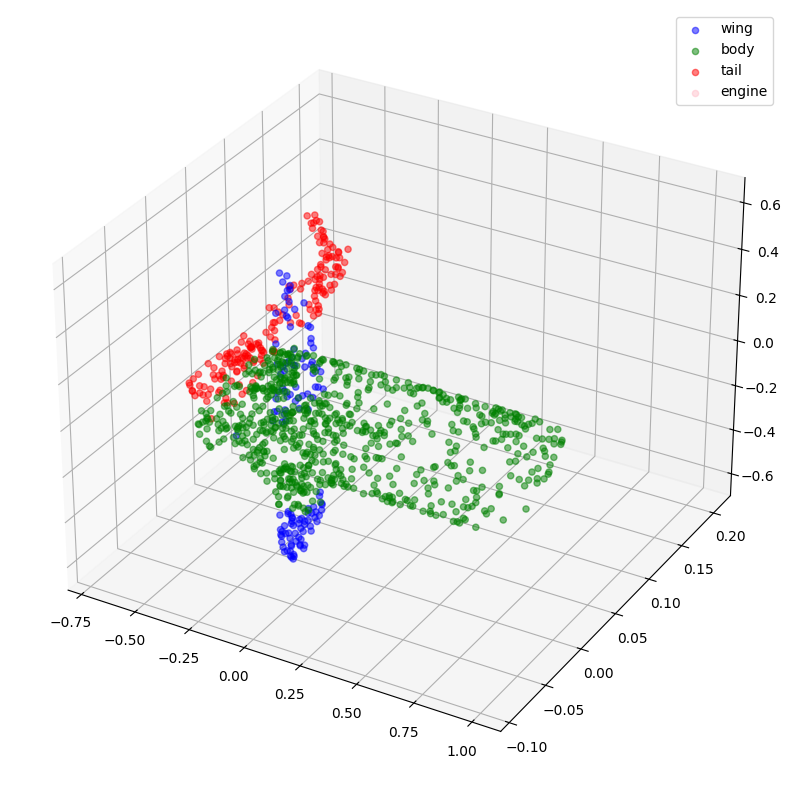
def visualize_single_point_cloud(point_clouds, label_clouds, idx):
label_map = LABELS + ["none"]
point_cloud = point_clouds[idx]
label_cloud = label_clouds[idx]
visualize_data(point_cloud, [label_map[np.argmax(label)] for label in label_cloud])
idx = np.random.choice(len(validation_batch[0]))
print(f"Index selected: {idx}")
# Plotting with ground-truth.
visualize_single_point_cloud(validation_batch[0], validation_batch[1], idx)
# Plotting with predicted labels.
visualize_single_point_cloud(validation_batch[0], val_predictions, idx)
1/1 ━━━━━━━━━━━━━━━━━━━━ 1s 1s/step
Validation prediction shape: (32, 1024, 5)
Index selected: 26
最终说明
如果您有兴趣了解有关此主题的更多信息，您可能会发现这个仓库很有用。