无
使用 Vision Transformer 进行目标检测
作者: Karan V. Dave
创建日期 2022/03/27
上次修改 2023/11/20
描述: 使用 Vision Transformer 进行目标检测的简单 Keras 实现。
引言
Alexey Dosovitskiy 等人的文章 Vision Transformer (ViT) 架构表明,将纯 Transformer 直接应用于图像块序列可以在目标检测任务中表现良好。
在本 Keras 示例中,我们实现了用于目标检测的 ViT,并在 Caltech 101 数据集上对其进行训练,以检测给定图像中的飞机。
导入和设置
import os
os.environ["KERAS_BACKEND"] = "jax" # @param ["tensorflow", "jax", "torch"]
import numpy as np
import keras
from keras import layers
from keras import ops
import matplotlib.pyplot as plt
import numpy as np
import cv2
import os
import scipy.io
import shutil
准备数据集
我们使用 Caltech 101 数据集。
# Path to images and annotations
path_images = "./101_ObjectCategories/airplanes/"
path_annot = "./Annotations/Airplanes_Side_2/"
path_to_downloaded_file = keras.utils.get_file(
fname="caltech_101_zipped",
origin="https://data.caltech.edu/records/mzrjq-6wc02/files/caltech-101.zip",
extract=True,
archive_format="zip", # downloaded file format
cache_dir="/", # cache and extract in current directory
)
download_base_dir = os.path.dirname(path_to_downloaded_file)
# Extracting tar files found inside main zip file
shutil.unpack_archive(
os.path.join(download_base_dir, "caltech-101", "101_ObjectCategories.tar.gz"), "."
)
shutil.unpack_archive(
os.path.join(download_base_dir, "caltech-101", "Annotations.tar"), "."
)
# list of paths to images and annotations
image_paths = [
f for f in os.listdir(path_images) if os.path.isfile(os.path.join(path_images, f))
]
annot_paths = [
f for f in os.listdir(path_annot) if os.path.isfile(os.path.join(path_annot, f))
]
image_paths.sort()
annot_paths.sort()
image_size = 224 # resize input images to this size
images, targets = [], []
# loop over the annotations and images, preprocess them and store in lists
for i in range(0, len(annot_paths)):
# Access bounding box coordinates
annot = scipy.io.loadmat(path_annot + annot_paths[i])["box_coord"][0]
top_left_x, top_left_y = annot[2], annot[0]
bottom_right_x, bottom_right_y = annot[3], annot[1]
image = keras.utils.load_img(
path_images + image_paths[i],
)
(w, h) = image.size[:2]
# resize images
image = image.resize((image_size, image_size))
# convert image to array and append to list
images.append(keras.utils.img_to_array(image))
# apply relative scaling to bounding boxes as per given image and append to list
targets.append(
(
float(top_left_x) / w,
float(top_left_y) / h,
float(bottom_right_x) / w,
float(bottom_right_y) / h,
)
)
# Convert the list to numpy array, split to train and test dataset
(x_train), (y_train) = (
np.asarray(images[: int(len(images) * 0.8)]),
np.asarray(targets[: int(len(targets) * 0.8)]),
)
(x_test), (y_test) = (
np.asarray(images[int(len(images) * 0.8) :]),
np.asarray(targets[int(len(targets) * 0.8) :]),
)
实现多层感知机(MLP)
我们参考了 Keras 示例 使用 Vision Transformer 的图像分类 中的代码。
def mlp(x, hidden_units, dropout_rate):
for units in hidden_units:
x = layers.Dense(units, activation=keras.activations.gelu)(x)
x = layers.Dropout(dropout_rate)(x)
return x
实现图像块创建层
class Patches(layers.Layer):
def __init__(self, patch_size):
super().__init__()
self.patch_size = patch_size
def call(self, images):
input_shape = ops.shape(images)
batch_size = input_shape[0]
height = input_shape[1]
width = input_shape[2]
channels = input_shape[3]
num_patches_h = height // self.patch_size
num_patches_w = width // self.patch_size
patches = keras.ops.image.extract_patches(images, size=self.patch_size)
patches = ops.reshape(
patches,
(
batch_size,
num_patches_h * num_patches_w,
self.patch_size * self.patch_size * channels,
),
)
return patches
def get_config(self):
config = super().get_config()
config.update({"patch_size": self.patch_size})
return config
显示输入图像的图像块
patch_size = 32 # Size of the patches to be extracted from the input images
plt.figure(figsize=(4, 4))
plt.imshow(x_train[0].astype("uint8"))
plt.axis("off")
patches = Patches(patch_size)(np.expand_dims(x_train[0], axis=0))
print(f"Image size: {image_size} X {image_size}")
print(f"Patch size: {patch_size} X {patch_size}")
print(f"{patches.shape[1]} patches per image \n{patches.shape[-1]} elements per patch")
n = int(np.sqrt(patches.shape[1]))
plt.figure(figsize=(4, 4))
for i, patch in enumerate(patches[0]):
ax = plt.subplot(n, n, i + 1)
patch_img = ops.reshape(patch, (patch_size, patch_size, 3))
plt.imshow(ops.convert_to_numpy(patch_img).astype("uint8"))
plt.axis("off")
Image size: 224 X 224
Patch size: 32 X 32
49 patches per image
3072 elements per patch


实现图像块编码层
PatchEncoder 层通过将图像块投影到大小为 projection_dim 的向量来进行线性变换。它还会向投影向量添加可学习的位置编码。
class PatchEncoder(layers.Layer):
def __init__(self, num_patches, projection_dim):
super().__init__()
self.num_patches = num_patches
self.projection = layers.Dense(units=projection_dim)
self.position_embedding = layers.Embedding(
input_dim=num_patches, output_dim=projection_dim
)
# Override function to avoid error while saving model
def get_config(self):
config = super().get_config().copy()
config.update(
{
"input_shape": input_shape,
"patch_size": patch_size,
"num_patches": num_patches,
"projection_dim": projection_dim,
"num_heads": num_heads,
"transformer_units": transformer_units,
"transformer_layers": transformer_layers,
"mlp_head_units": mlp_head_units,
}
)
return config
def call(self, patch):
positions = ops.expand_dims(
ops.arange(start=0, stop=self.num_patches, step=1), axis=0
)
projected_patches = self.projection(patch)
encoded = projected_patches + self.position_embedding(positions)
return encoded
构建 ViT 模型
ViT 模型包含多个 Transformer 块。MultiHeadAttention 层用于自注意力,应用于图像块序列。编码后的图像块(跳跃连接)和自注意力层输出经过归一化后输入多层感知机(MLP)。模型输出表示对象边界框坐标的四个维度。
def create_vit_object_detector(
input_shape,
patch_size,
num_patches,
projection_dim,
num_heads,
transformer_units,
transformer_layers,
mlp_head_units,
):
inputs = keras.Input(shape=input_shape)
# Create patches
patches = Patches(patch_size)(inputs)
# Encode patches
encoded_patches = PatchEncoder(num_patches, projection_dim)(patches)
# Create multiple layers of the Transformer block.
for _ in range(transformer_layers):
# Layer normalization 1.
x1 = layers.LayerNormalization(epsilon=1e-6)(encoded_patches)
# Create a multi-head attention layer.
attention_output = layers.MultiHeadAttention(
num_heads=num_heads, key_dim=projection_dim, dropout=0.1
)(x1, x1)
# Skip connection 1.
x2 = layers.Add()([attention_output, encoded_patches])
# Layer normalization 2.
x3 = layers.LayerNormalization(epsilon=1e-6)(x2)
# MLP
x3 = mlp(x3, hidden_units=transformer_units, dropout_rate=0.1)
# Skip connection 2.
encoded_patches = layers.Add()([x3, x2])
# Create a [batch_size, projection_dim] tensor.
representation = layers.LayerNormalization(epsilon=1e-6)(encoded_patches)
representation = layers.Flatten()(representation)
representation = layers.Dropout(0.3)(representation)
# Add MLP.
features = mlp(representation, hidden_units=mlp_head_units, dropout_rate=0.3)
bounding_box = layers.Dense(4)(
features
) # Final four neurons that output bounding box
# return Keras model.
return keras.Model(inputs=inputs, outputs=bounding_box)
运行实验
def run_experiment(model, learning_rate, weight_decay, batch_size, num_epochs):
optimizer = keras.optimizers.AdamW(
learning_rate=learning_rate, weight_decay=weight_decay
)
# Compile model.
model.compile(optimizer=optimizer, loss=keras.losses.MeanSquaredError())
checkpoint_filepath = "vit_object_detector.weights.h5"
checkpoint_callback = keras.callbacks.ModelCheckpoint(
checkpoint_filepath,
monitor="val_loss",
save_best_only=True,
save_weights_only=True,
)
history = model.fit(
x=x_train,
y=y_train,
batch_size=batch_size,
epochs=num_epochs,
validation_split=0.1,
callbacks=[
checkpoint_callback,
keras.callbacks.EarlyStopping(monitor="val_loss", patience=10),
],
)
return history
input_shape = (image_size, image_size, 3) # input image shape
learning_rate = 0.001
weight_decay = 0.0001
batch_size = 32
num_epochs = 100
num_patches = (image_size // patch_size) ** 2
projection_dim = 64
num_heads = 4
# Size of the transformer layers
transformer_units = [
projection_dim * 2,
projection_dim,
]
transformer_layers = 4
mlp_head_units = [2048, 1024, 512, 64, 32] # Size of the dense layers
history = []
num_patches = (image_size // patch_size) ** 2
vit_object_detector = create_vit_object_detector(
input_shape,
patch_size,
num_patches,
projection_dim,
num_heads,
transformer_units,
transformer_layers,
mlp_head_units,
)
# Train model
history = run_experiment(
vit_object_detector, learning_rate, weight_decay, batch_size, num_epochs
)
def plot_history(item):
plt.plot(history.history[item], label=item)
plt.plot(history.history["val_" + item], label="val_" + item)
plt.xlabel("Epochs")
plt.ylabel(item)
plt.title("Train and Validation {} Over Epochs".format(item), fontsize=14)
plt.legend()
plt.grid()
plt.show()
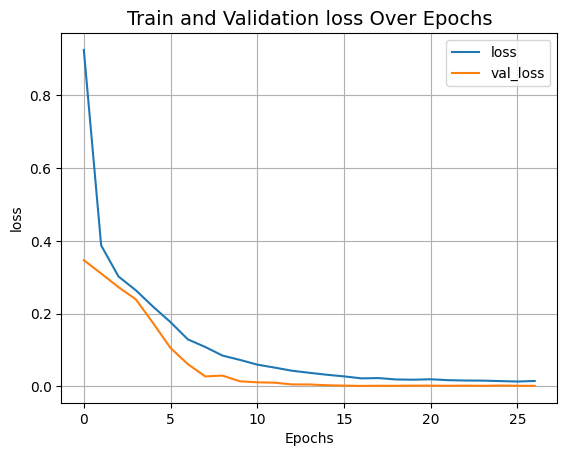
plot_history("loss")
Epoch 1/100
18/18 ━━━━━━━━━━━━━━━━━━━━ 9s 109ms/step - loss: 1.2097 - val_loss: 0.3468
Epoch 2/100
18/18 ━━━━━━━━━━━━━━━━━━━━ 0s 25ms/step - loss: 0.4260 - val_loss: 0.3102
Epoch 3/100
18/18 ━━━━━━━━━━━━━━━━━━━━ 0s 25ms/step - loss: 0.3268 - val_loss: 0.2727
Epoch 4/100
18/18 ━━━━━━━━━━━━━━━━━━━━ 0s 25ms/step - loss: 0.2815 - val_loss: 0.2391
Epoch 5/100
18/18 ━━━━━━━━━━━━━━━━━━━━ 0s 25ms/step - loss: 0.2290 - val_loss: 0.1735
Epoch 6/100
18/18 ━━━━━━━━━━━━━━━━━━━━ 0s 24ms/step - loss: 0.1870 - val_loss: 0.1055
Epoch 7/100
18/18 ━━━━━━━━━━━━━━━━━━━━ 0s 25ms/step - loss: 0.1401 - val_loss: 0.0610
Epoch 8/100
18/18 ━━━━━━━━━━━━━━━━━━━━ 0s 25ms/step - loss: 0.1122 - val_loss: 0.0274
Epoch 9/100
18/18 ━━━━━━━━━━━━━━━━━━━━ 0s 8ms/step - loss: 0.0924 - val_loss: 0.0296
Epoch 10/100
18/18 ━━━━━━━━━━━━━━━━━━━━ 0s 24ms/step - loss: 0.0765 - val_loss: 0.0139
Epoch 11/100
18/18 ━━━━━━━━━━━━━━━━━━━━ 0s 25ms/step - loss: 0.0597 - val_loss: 0.0111
Epoch 12/100
18/18 ━━━━━━━━━━━━━━━━━━━━ 0s 25ms/step - loss: 0.0540 - val_loss: 0.0101
Epoch 13/100
18/18 ━━━━━━━━━━━━━━━━━━━━ 0s 24ms/step - loss: 0.0432 - val_loss: 0.0053
Epoch 14/100
18/18 ━━━━━━━━━━━━━━━━━━━━ 0s 24ms/step - loss: 0.0380 - val_loss: 0.0052
Epoch 15/100
18/18 ━━━━━━━━━━━━━━━━━━━━ 0s 25ms/step - loss: 0.0334 - val_loss: 0.0030
Epoch 16/100
18/18 ━━━━━━━━━━━━━━━━━━━━ 0s 25ms/step - loss: 0.0283 - val_loss: 0.0021
Epoch 17/100
18/18 ━━━━━━━━━━━━━━━━━━━━ 0s 24ms/step - loss: 0.0228 - val_loss: 0.0012
Epoch 18/100
18/18 ━━━━━━━━━━━━━━━━━━━━ 0s 8ms/step - loss: 0.0244 - val_loss: 0.0017
Epoch 19/100
18/18 ━━━━━━━━━━━━━━━━━━━━ 0s 8ms/step - loss: 0.0195 - val_loss: 0.0016
Epoch 20/100
18/18 ━━━━━━━━━━━━━━━━━━━━ 0s 8ms/step - loss: 0.0189 - val_loss: 0.0020
Epoch 21/100
18/18 ━━━━━━━━━━━━━━━━━━━━ 0s 8ms/step - loss: 0.0191 - val_loss: 0.0019
Epoch 22/100
18/18 ━━━━━━━━━━━━━━━━━━━━ 0s 8ms/step - loss: 0.0174 - val_loss: 0.0016
Epoch 23/100
18/18 ━━━━━━━━━━━━━━━━━━━━ 0s 8ms/step - loss: 0.0157 - val_loss: 0.0020
Epoch 24/100
18/18 ━━━━━━━━━━━━━━━━━━━━ 0s 8ms/step - loss: 0.0157 - val_loss: 0.0015
Epoch 25/100
18/18 ━━━━━━━━━━━━━━━━━━━━ 0s 8ms/step - loss: 0.0139 - val_loss: 0.0023
Epoch 26/100
18/18 ━━━━━━━━━━━━━━━━━━━━ 0s 8ms/step - loss: 0.0130 - val_loss: 0.0017
Epoch 27/100
18/18 ━━━━━━━━━━━━━━━━━━━━ 0s 8ms/step - loss: 0.0157 - val_loss: 0.0014
评估模型
import matplotlib.patches as patches
# Saves the model in current path
vit_object_detector.save("vit_object_detector.keras")
# To calculate IoU (intersection over union, given two bounding boxes)
def bounding_box_intersection_over_union(box_predicted, box_truth):
# get (x, y) coordinates of intersection of bounding boxes
top_x_intersect = max(box_predicted[0], box_truth[0])
top_y_intersect = max(box_predicted[1], box_truth[1])
bottom_x_intersect = min(box_predicted[2], box_truth[2])
bottom_y_intersect = min(box_predicted[3], box_truth[3])
# calculate area of the intersection bb (bounding box)
intersection_area = max(0, bottom_x_intersect - top_x_intersect + 1) * max(
0, bottom_y_intersect - top_y_intersect + 1
)
# calculate area of the prediction bb and ground-truth bb
box_predicted_area = (box_predicted[2] - box_predicted[0] + 1) * (
box_predicted[3] - box_predicted[1] + 1
)
box_truth_area = (box_truth[2] - box_truth[0] + 1) * (
box_truth[3] - box_truth[1] + 1
)
# calculate intersection over union by taking intersection
# area and dividing it by the sum of predicted bb and ground truth
# bb areas subtracted by the interesection area
# return ioU
return intersection_area / float(
box_predicted_area + box_truth_area - intersection_area
)
i, mean_iou = 0, 0
# Compare results for 10 images in the test set
for input_image in x_test[:10]:
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(15, 15))
im = input_image
# Display the image
ax1.imshow(im.astype("uint8"))
ax2.imshow(im.astype("uint8"))
input_image = cv2.resize(
input_image, (image_size, image_size), interpolation=cv2.INTER_AREA
)
input_image = np.expand_dims(input_image, axis=0)
preds = vit_object_detector.predict(input_image)[0]
(h, w) = (im).shape[0:2]
top_left_x, top_left_y = int(preds[0] * w), int(preds[1] * h)
bottom_right_x, bottom_right_y = int(preds[2] * w), int(preds[3] * h)
box_predicted = [top_left_x, top_left_y, bottom_right_x, bottom_right_y]
# Create the bounding box
rect = patches.Rectangle(
(top_left_x, top_left_y),
bottom_right_x - top_left_x,
bottom_right_y - top_left_y,
facecolor="none",
edgecolor="red",
linewidth=1,
)
# Add the bounding box to the image
ax1.add_patch(rect)
ax1.set_xlabel(
"Predicted: "
+ str(top_left_x)
+ ", "
+ str(top_left_y)
+ ", "
+ str(bottom_right_x)
+ ", "
+ str(bottom_right_y)
)
top_left_x, top_left_y = int(y_test[i][0] * w), int(y_test[i][1] * h)
bottom_right_x, bottom_right_y = int(y_test[i][2] * w), int(y_test[i][3] * h)
box_truth = top_left_x, top_left_y, bottom_right_x, bottom_right_y
mean_iou += bounding_box_intersection_over_union(box_predicted, box_truth)
# Create the bounding box
rect = patches.Rectangle(
(top_left_x, top_left_y),
bottom_right_x - top_left_x,
bottom_right_y - top_left_y,
facecolor="none",
edgecolor="red",
linewidth=1,
)
# Add the bounding box to the image
ax2.add_patch(rect)
ax2.set_xlabel(
"Target: "
+ str(top_left_x)
+ ", "
+ str(top_left_y)
+ ", "
+ str(bottom_right_x)
+ ", "
+ str(bottom_right_y)
+ "\n"
+ "IoU"
+ str(bounding_box_intersection_over_union(box_predicted, box_truth))
)
i = i + 1
print("mean_iou: " + str(mean_iou / len(x_test[:10])))
plt.show()
1/1 ━━━━━━━━━━━━━━━━━━━━ 1s 1s/step
1/1 ━━━━━━━━━━━━━━━━━━━━ 0s 1ms/step
1/1 ━━━━━━━━━━━━━━━━━━━━ 0s 1ms/step
1/1 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step
1/1 ━━━━━━━━━━━━━━━━━━━━ 0s 1ms/step
1/1 ━━━━━━━━━━━━━━━━━━━━ 0s 1ms/step
1/1 ━━━━━━━━━━━━━━━━━━━━ 0s 1ms/step
1/1 ━━━━━━━━━━━━━━━━━━━━ 0s 1ms/step
1/1 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step
1/1 ━━━━━━━━━━━━━━━━━━━━ 0s 1ms/step
mean_iou: 0.9092338486331416

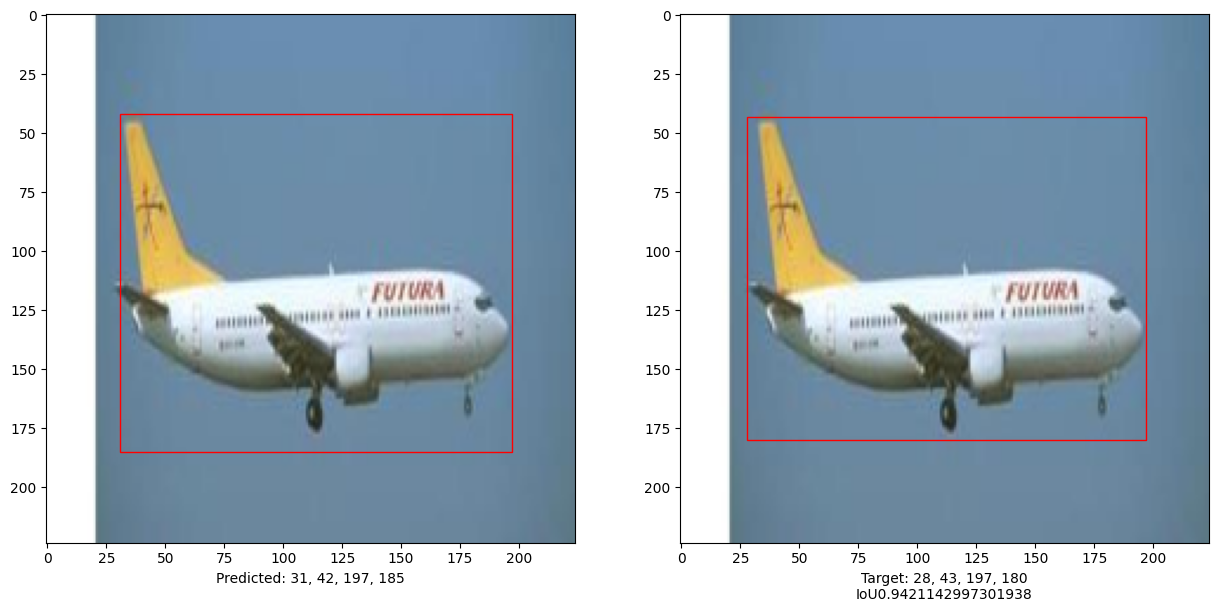
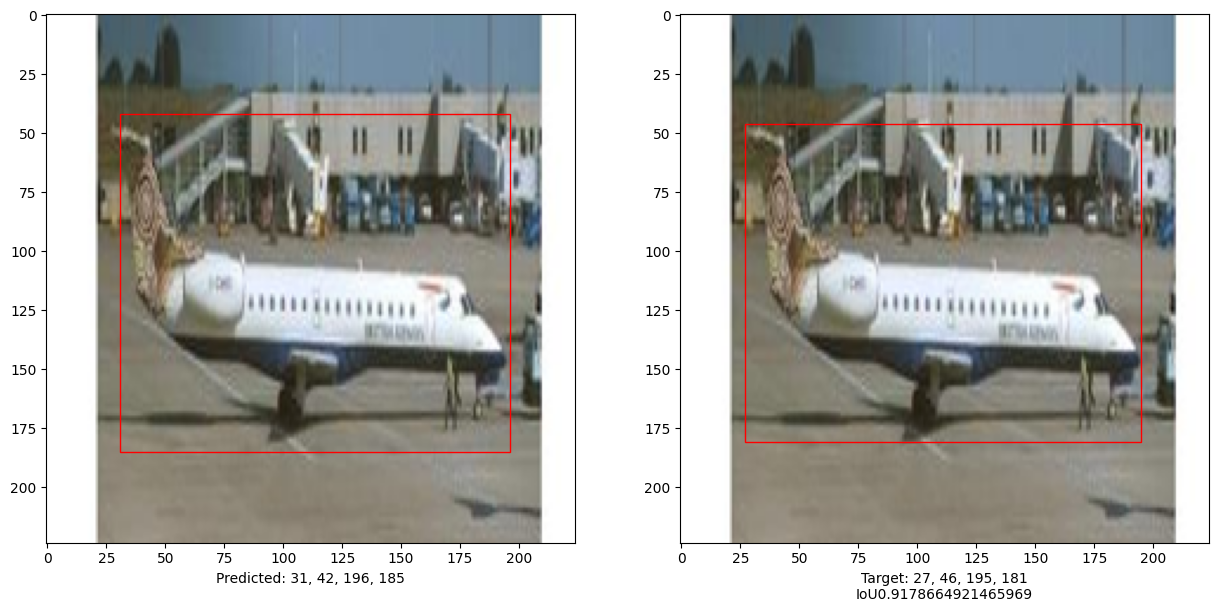
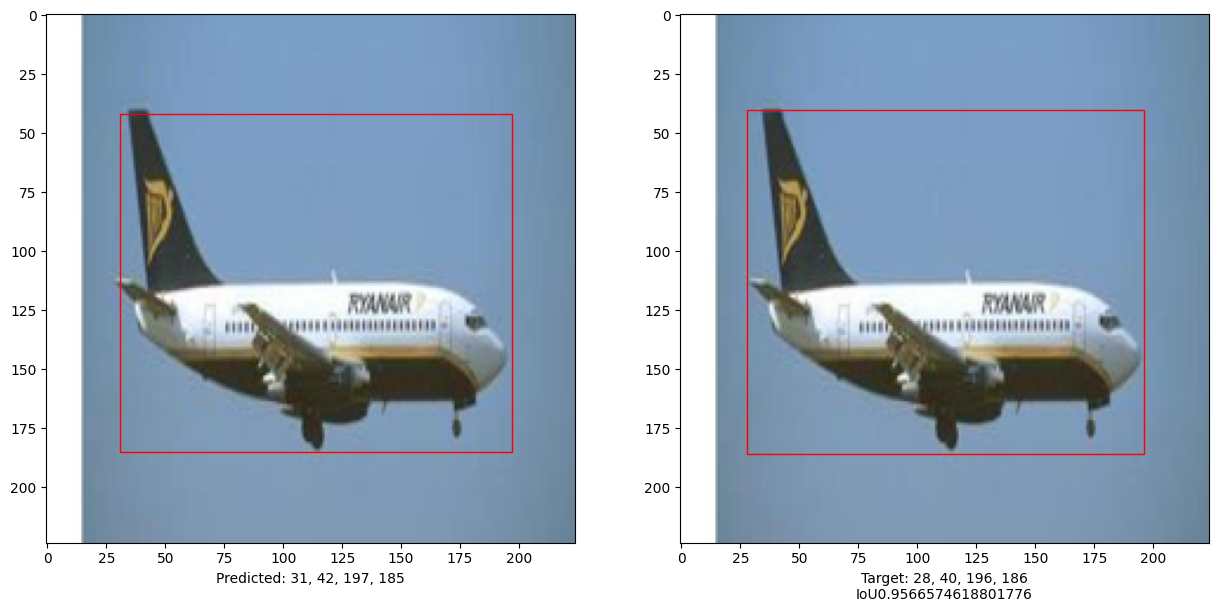
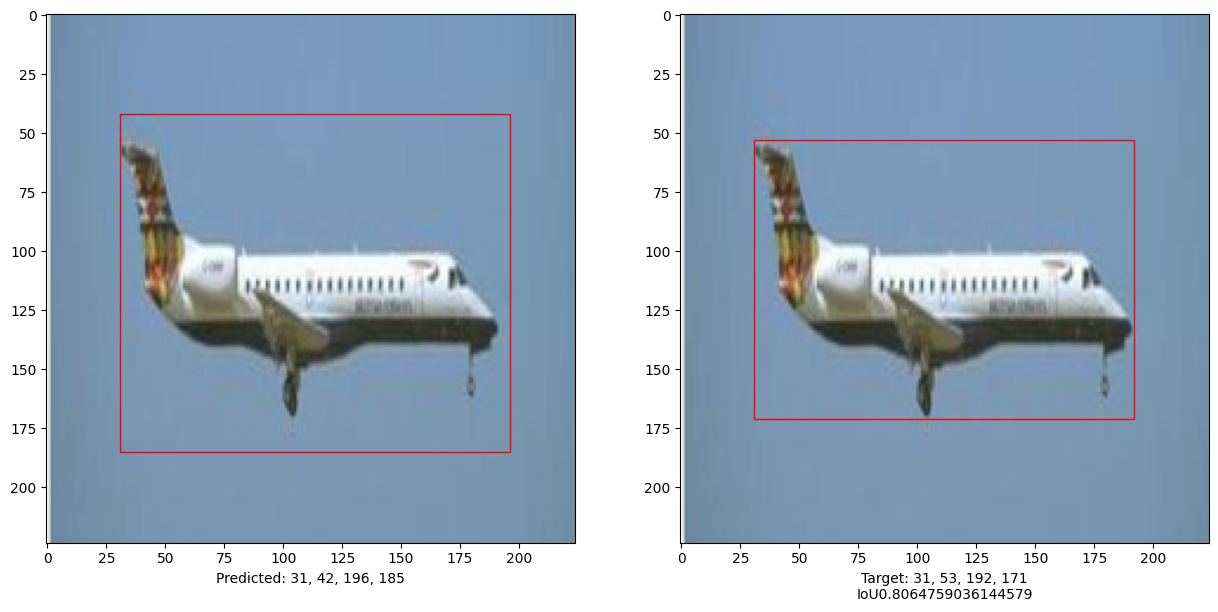
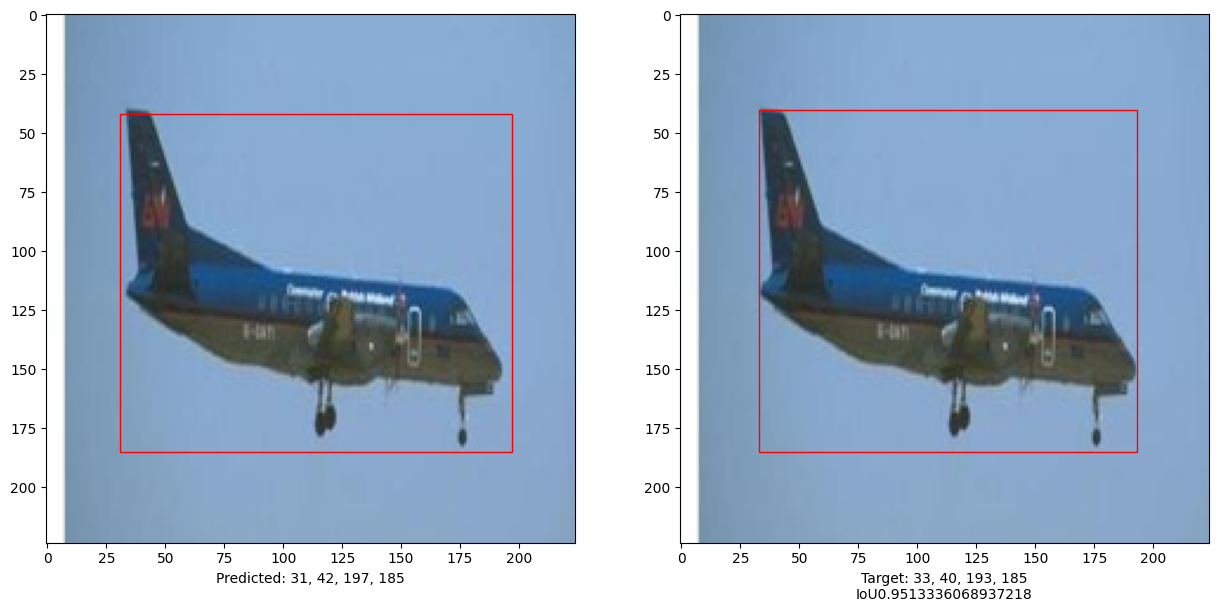
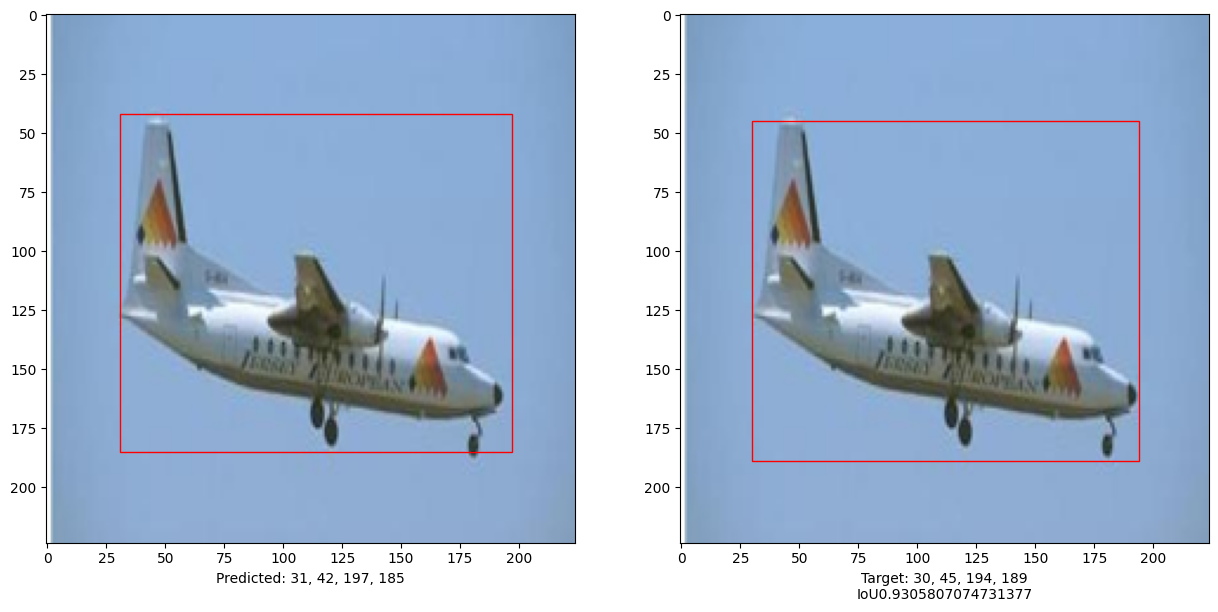
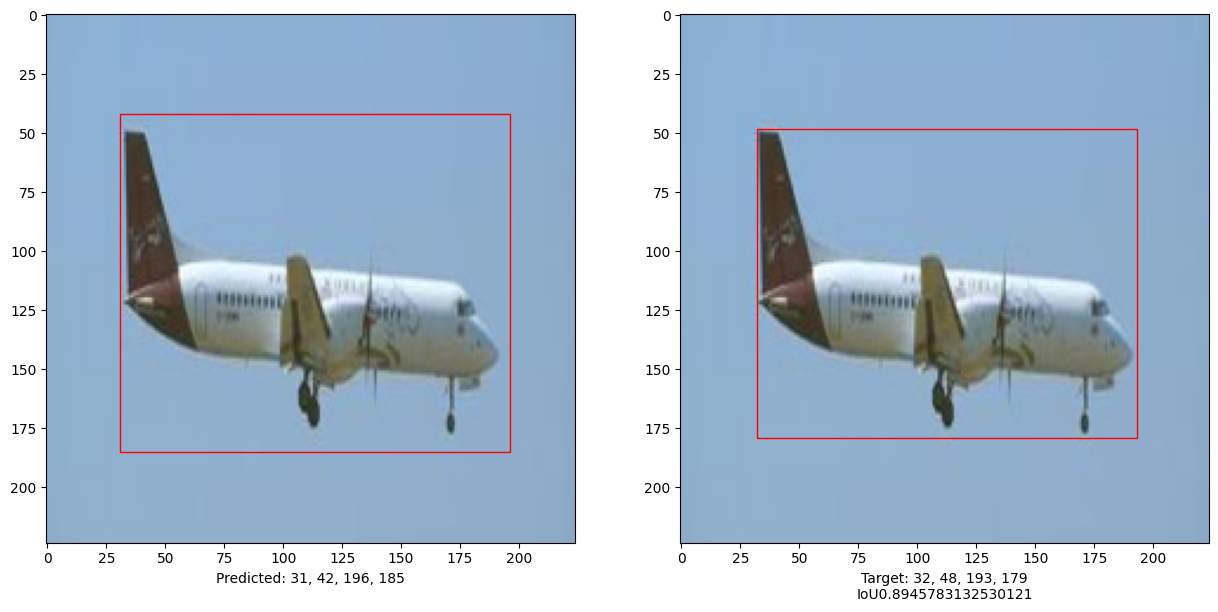

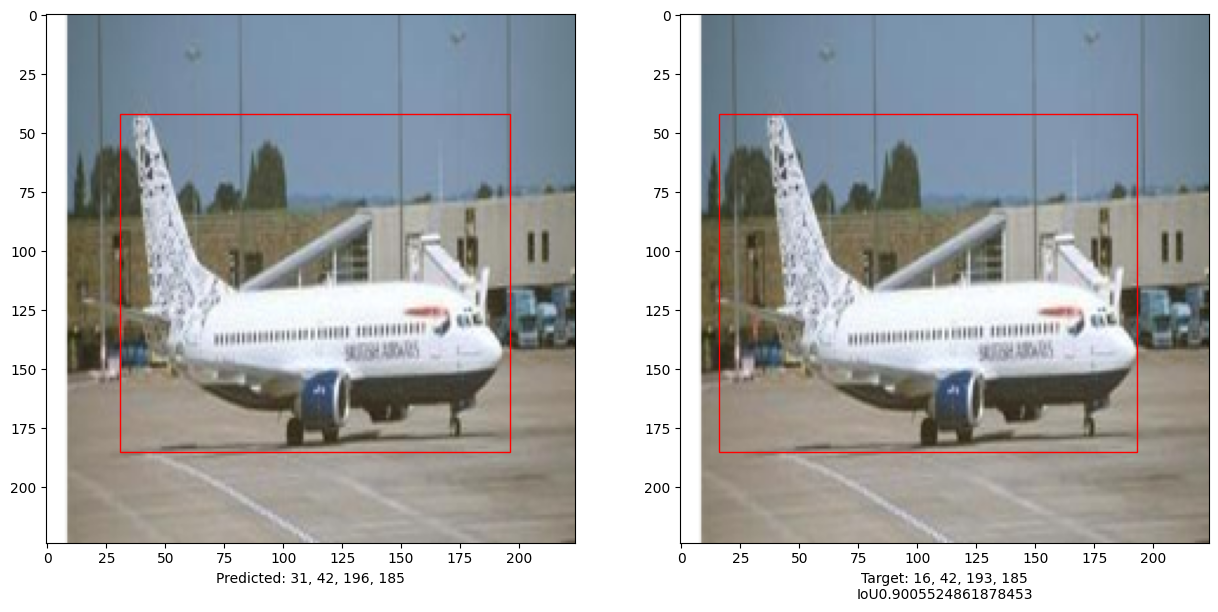
本示例演示了可以训练一个纯 Transformer 来预测给定图像中对象的边界框,从而将 Transformer 的用途扩展到目标检测任务。通过调整超参数和进行预训练可以进一步改进模型。