度量学习用于图像相似度搜索
作者: Mat Kelcey
创建日期 2020/06/05
最后修改日期 2020/06/09
描述: 在 CIFAR-10 图像上使用相似度度量学习的示例。
概述
度量学习旨在训练模型,将输入嵌入高维空间中,使得训练方案中定义的“相似”输入彼此靠近。训练好的模型可以为下游系统生成嵌入,这些系统对相似度有需求;例如,可将其用作搜索的排序信号,或作为另一个监督问题的预训练嵌入模型。
有关度量学习的更详细概述,请参阅
设置
将 Keras 后端设置为 tensorflow。
import os
os.environ["KERAS_BACKEND"] = "tensorflow"
import random
import matplotlib.pyplot as plt
import numpy as np
import tensorflow as tf
from collections import defaultdict
from PIL import Image
from sklearn.metrics import ConfusionMatrixDisplay
import keras
from keras import layers
数据集
本示例将使用 CIFAR-10 数据集。
from keras.datasets import cifar10
(x_train, y_train), (x_test, y_test) = cifar10.load_data()
x_train = x_train.astype("float32") / 255.0
y_train = np.squeeze(y_train)
x_test = x_test.astype("float32") / 255.0
y_test = np.squeeze(y_test)
为了了解数据集,我们可以可视化展示 25 个随机样本的网格。
height_width = 32
def show_collage(examples):
box_size = height_width + 2
num_rows, num_cols = examples.shape[:2]
collage = Image.new(
mode="RGB",
size=(num_cols * box_size, num_rows * box_size),
color=(250, 250, 250),
)
for row_idx in range(num_rows):
for col_idx in range(num_cols):
array = (np.array(examples[row_idx, col_idx]) * 255).astype(np.uint8)
collage.paste(
Image.fromarray(array), (col_idx * box_size, row_idx * box_size)
)
# Double size for visualisation.
collage = collage.resize((2 * num_cols * box_size, 2 * num_rows * box_size))
return collage
# Show a collage of 5x5 random images.
sample_idxs = np.random.randint(0, 50000, size=(5, 5))
examples = x_train[sample_idxs]
show_collage(examples)

度量学习提供的训练数据不是显式的 (X, y) 对,而是使用在表达相似度方面相关联的多个实例。在我们的示例中,我们将使用同一类别的实例来表示相似度;单个训练实例不会是一张图片,而是同一类别的两张图片。当提及这对图片时,我们将使用度量学习中常用的名称:anchor(随机选择的一张图片)和 positive(随机选择的另一张同一类别的图片)。
为了方便起见,我们需要建立一个查找表,将类别映射到该类别的实例。生成训练数据时,我们将从这个查找表中进行采样。
class_idx_to_train_idxs = defaultdict(list)
for y_train_idx, y in enumerate(y_train):
class_idx_to_train_idxs[y].append(y_train_idx)
class_idx_to_test_idxs = defaultdict(list)
for y_test_idx, y in enumerate(y_test):
class_idx_to_test_idxs[y].append(y_test_idx)
本示例采用最简单的训练方法;一个批次将包含分布在不同类别中的 (anchor, positive) 对。学习的目标是将 anchor 和 positive 对拉得更近,同时使其远离批次中的其他实例。在这种情况下,批次大小将由类别的数量决定;对于 CIFAR-10 来说,这个数量是 10。
num_classes = 10
class AnchorPositivePairs(keras.utils.Sequence):
def __init__(self, num_batches):
super().__init__()
self.num_batches = num_batches
def __len__(self):
return self.num_batches
def __getitem__(self, _idx):
x = np.empty((2, num_classes, height_width, height_width, 3), dtype=np.float32)
for class_idx in range(num_classes):
examples_for_class = class_idx_to_train_idxs[class_idx]
anchor_idx = random.choice(examples_for_class)
positive_idx = random.choice(examples_for_class)
while positive_idx == anchor_idx:
positive_idx = random.choice(examples_for_class)
x[0, class_idx] = x_train[anchor_idx]
x[1, class_idx] = x_train[positive_idx]
return x
我们可以通过另一张拼贴画来可视化一个批次。顶行显示的是从 10 个类别中随机选择的 anchor,底行显示的是相应的 10 个 positive。
examples = next(iter(AnchorPositivePairs(num_batches=1)))
show_collage(examples)

嵌入模型
我们定义了一个带有自定义 train_step 的模型,该模型首先嵌入 anchor 和 positive,然后使用它们的成对点积作为 softmax 的 logits。
class EmbeddingModel(keras.Model):
def train_step(self, data):
# Note: Workaround for open issue, to be removed.
if isinstance(data, tuple):
data = data[0]
anchors, positives = data[0], data[1]
with tf.GradientTape() as tape:
# Run both anchors and positives through model.
anchor_embeddings = self(anchors, training=True)
positive_embeddings = self(positives, training=True)
# Calculate cosine similarity between anchors and positives. As they have
# been normalised this is just the pair wise dot products.
similarities = keras.ops.einsum(
"ae,pe->ap", anchor_embeddings, positive_embeddings
)
# Since we intend to use these as logits we scale them by a temperature.
# This value would normally be chosen as a hyper parameter.
temperature = 0.2
similarities /= temperature
# We use these similarities as logits for a softmax. The labels for
# this call are just the sequence [0, 1, 2, ..., num_classes] since we
# want the main diagonal values, which correspond to the anchor/positive
# pairs, to be high. This loss will move embeddings for the
# anchor/positive pairs together and move all other pairs apart.
sparse_labels = keras.ops.arange(num_classes)
loss = self.compute_loss(y=sparse_labels, y_pred=similarities)
# Calculate gradients and apply via optimizer.
gradients = tape.gradient(loss, self.trainable_variables)
self.optimizer.apply_gradients(zip(gradients, self.trainable_variables))
# Update and return metrics (specifically the one for the loss value).
for metric in self.metrics:
# Calling `self.compile` will by default add a [`keras.metrics.Mean`](/api/metrics/metrics_wrappers#mean-class) loss
if metric.name == "loss":
metric.update_state(loss)
else:
metric.update_state(sparse_labels, similarities)
return {m.name: m.result() for m in self.metrics}
接下来,我们描述将图像映射到嵌入的架构。该模型由一系列 2D 卷积层、全局池化层以及最终投射到嵌入空间的线性层组成。在度量学习中,通常会对嵌入进行归一化,以便使用简单的点积来衡量相似度。为了简单起见,该模型故意设计得很小。
inputs = layers.Input(shape=(height_width, height_width, 3))
x = layers.Conv2D(filters=32, kernel_size=3, strides=2, activation="relu")(inputs)
x = layers.Conv2D(filters=64, kernel_size=3, strides=2, activation="relu")(x)
x = layers.Conv2D(filters=128, kernel_size=3, strides=2, activation="relu")(x)
x = layers.GlobalAveragePooling2D()(x)
embeddings = layers.Dense(units=8, activation=None)(x)
embeddings = layers.UnitNormalization()(embeddings)
model = EmbeddingModel(inputs, embeddings)
最后,我们运行训练。在 Google Colab GPU 实例上,这大约需要一分钟。
model.compile(
optimizer=keras.optimizers.Adam(learning_rate=1e-3),
loss=keras.losses.SparseCategoricalCrossentropy(from_logits=True),
)
history = model.fit(AnchorPositivePairs(num_batches=1000), epochs=20)
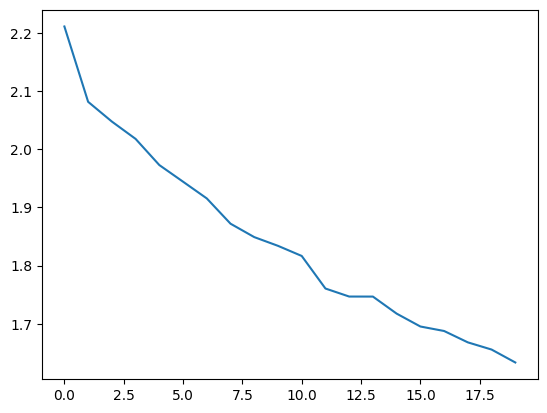
plt.plot(history.history["loss"])
plt.show()
Epoch 1/20
77/1000 ━[37m━━━━━━━━━━━━━━━━━━━ 1s 2ms/step - loss: 2.2962
WARNING: All log messages before absl::InitializeLog() is called are written to STDERR
I0000 00:00:1700589927.295343 3724442 device_compiler.h:187] Compiled cluster using XLA! This line is logged at most once for the lifetime of the process.
1000/1000 ━━━━━━━━━━━━━━━━━━━━ 6s 2ms/step - loss: 2.2504
Epoch 2/20
1000/1000 ━━━━━━━━━━━━━━━━━━━━ 2s 2ms/step - loss: 2.1068
Epoch 3/20
1000/1000 ━━━━━━━━━━━━━━━━━━━━ 2s 2ms/step - loss: 2.0646
Epoch 4/20
1000/1000 ━━━━━━━━━━━━━━━━━━━━ 2s 2ms/step - loss: 2.0210
Epoch 5/20
1000/1000 ━━━━━━━━━━━━━━━━━━━━ 2s 2ms/step - loss: 1.9857
Epoch 6/20
1000/1000 ━━━━━━━━━━━━━━━━━━━━ 2s 2ms/step - loss: 1.9543
Epoch 7/20
1000/1000 ━━━━━━━━━━━━━━━━━━━━ 2s 2ms/step - loss: 1.9175
Epoch 8/20
1000/1000 ━━━━━━━━━━━━━━━━━━━━ 2s 2ms/step - loss: 1.8740
Epoch 9/20
1000/1000 ━━━━━━━━━━━━━━━━━━━━ 2s 2ms/step - loss: 1.8474
Epoch 10/20
1000/1000 ━━━━━━━━━━━━━━━━━━━━ 2s 2ms/step - loss: 1.8380
Epoch 11/20
1000/1000 ━━━━━━━━━━━━━━━━━━━━ 2s 2ms/step - loss: 1.8146
Epoch 12/20
1000/1000 ━━━━━━━━━━━━━━━━━━━━ 2s 2ms/step - loss: 1.7658
Epoch 13/20
1000/1000 ━━━━━━━━━━━━━━━━━━━━ 2s 2ms/step - loss: 1.7512
Epoch 14/20
1000/1000 ━━━━━━━━━━━━━━━━━━━━ 2s 2ms/step - loss: 1.7671
Epoch 15/20
1000/1000 ━━━━━━━━━━━━━━━━━━━━ 2s 2ms/step - loss: 1.7245
Epoch 16/20
1000/1000 ━━━━━━━━━━━━━━━━━━━━ 2s 2ms/step - loss: 1.7001
Epoch 17/20
1000/1000 ━━━━━━━━━━━━━━━━━━━━ 2s 2ms/step - loss: 1.7099
Epoch 18/20
1000/1000 ━━━━━━━━━━━━━━━━━━━━ 2s 2ms/step - loss: 1.6775
Epoch 19/20
1000/1000 ━━━━━━━━━━━━━━━━━━━━ 2s 2ms/step - loss: 1.6547
Epoch 20/20
1000/1000 ━━━━━━━━━━━━━━━━━━━━ 2s 2ms/step - loss: 1.6356
测试
我们可以通过将该模型应用于测试集并考虑嵌入空间中的近邻来评估其质量。
首先,我们对测试集进行嵌入并计算所有近邻。请注意,由于嵌入向量是单位长度的,我们可以通过点积计算余弦相似度。
near_neighbours_per_example = 10
embeddings = model.predict(x_test)
gram_matrix = np.einsum("ae,be->ab", embeddings, embeddings)
near_neighbours = np.argsort(gram_matrix.T)[:, -(near_neighbours_per_example + 1) :]
313/313 ━━━━━━━━━━━━━━━━━━━━ 1s 3ms/step
作为对这些嵌入向量的视觉检查,我们可以为 5 个随机样本构建一个近邻拼贴画。下图的第一列是随机选择的图片,接下来的 10 列按相似度顺序列出了最近的近邻。
num_collage_examples = 5
examples = np.empty(
(
num_collage_examples,
near_neighbours_per_example + 1,
height_width,
height_width,
3,
),
dtype=np.float32,
)
for row_idx in range(num_collage_examples):
examples[row_idx, 0] = x_test[row_idx]
anchor_near_neighbours = reversed(near_neighbours[row_idx][:-1])
for col_idx, nn_idx in enumerate(anchor_near_neighbours):
examples[row_idx, col_idx + 1] = x_test[nn_idx]
show_collage(examples)

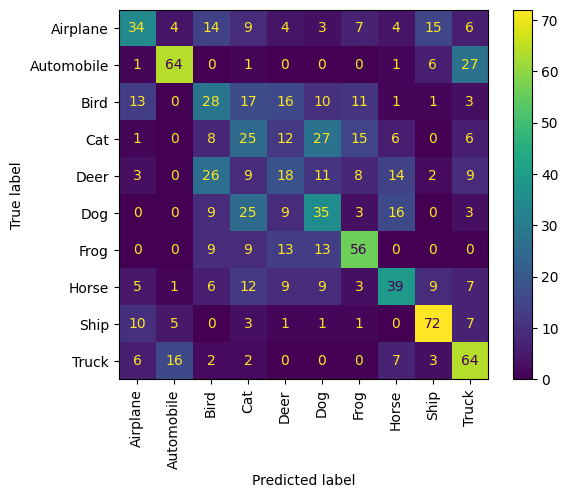
我们还可以通过混淆矩阵来量化评估近邻的正确性,从而了解模型的性能。
让我们从 10 个类别中每个类别抽取 10 个样本,并将其近邻视为一种预测;也就是说,该样本及其近邻是否属于同一类别?
我们观察到,每个动物类别通常表现良好,并且最容易与其他动物类别混淆。车辆类别也遵循相同的模式。
confusion_matrix = np.zeros((num_classes, num_classes))
# For each class.
for class_idx in range(num_classes):
# Consider 10 examples.
example_idxs = class_idx_to_test_idxs[class_idx][:10]
for y_test_idx in example_idxs:
# And count the classes of its near neighbours.
for nn_idx in near_neighbours[y_test_idx][:-1]:
nn_class_idx = y_test[nn_idx]
confusion_matrix[class_idx, nn_class_idx] += 1
# Display a confusion matrix.
labels = [
"Airplane",
"Automobile",
"Bird",
"Cat",
"Deer",
"Dog",
"Frog",
"Horse",
"Ship",
"Truck",
]
disp = ConfusionMatrixDisplay(confusion_matrix=confusion_matrix, display_labels=labels)
disp.plot(include_values=True, cmap="viridis", ax=None, xticks_rotation="vertical")
plt.show()