时间序列天气预报
作者: Prabhanshu Attri, Yashika Sharma, Kristi Takach, Falak Shah
创建日期 2020/06/23
最后修改日期 2023/11/22
描述: 本笔记本演示了如何使用 LSTM 模型进行时间序列预测。
设置
import pandas as pd
import matplotlib.pyplot as plt
import keras
气候数据时间序列
我们将使用 马克斯·普朗克生物地球化学研究所 记录的耶拿气候数据集。该数据集包含 14 个特征,如温度、压力、湿度等,每 10 分钟记录一次。
地点: 德国耶拿马克斯·普朗克生物地球化学研究所气象站
考虑的时间范围: 2009 年 1 月 10 日 - 2016 年 12 月 31 日
下表显示了列名、其值格式和描述。
| 索引 | 特征 | 格式 | 描述 |
|---|---|---|---|
| 1 | 日期时间 | 01.01.2009 00:10:00 | 日期-时间参照 |
| 2 | p (mbar) | 996.52 | 用于量化内部压力的帕斯卡国际单位。气象报告通常以毫巴表示大气压力。 |
| 3 | T (degC) | -8.02 | 摄氏温度 |
| 4 | Tpot (K) | 265.4 | 开尔文温度 |
| 5 | Tdew (degC) | -8.9 | 相对于湿度的摄氏温度。露点是空气中水分绝对量的测量值,DP 是空气无法容纳其所有水分并发生冷凝的温度。 |
| 6 | rh (%) | 93.3 | 相对湿度是衡量空气中水蒸气饱和程度的指标,%RH 决定了收集对象中水的含量。 |
| 7 | VPmax (mbar) | 3.33 | 饱和蒸汽压 |
| 8 | VPact (mbar) | 3.11 | 蒸汽压 |
| 9 | VPdef (mbar) | 0.22 | 蒸汽压亏缺 |
| 10 | sh (g/kg) | 1.94 | 比湿 |
| 11 | H2OC (mmol/mol) | 3.12 | 水蒸气浓度 |
| 12 | rho (g/m ** 3) | 1307.75 | 空气密度 |
| 13 | wv (m/s) | 1.03 | 风速 |
| 14 | max. wv (m/s) | 1.75 | 最大风速 |
| 15 | wd (deg) | 152.3 | 风向(度) |
from zipfile import ZipFile
uri = "https://storage.googleapis.com/tensorflow/tf-keras-datasets/jena_climate_2009_2016.csv.zip"
zip_path = keras.utils.get_file(origin=uri, fname="jena_climate_2009_2016.csv.zip")
zip_file = ZipFile(zip_path)
zip_file.extractall()
csv_path = "jena_climate_2009_2016.csv"
df = pd.read_csv(csv_path)
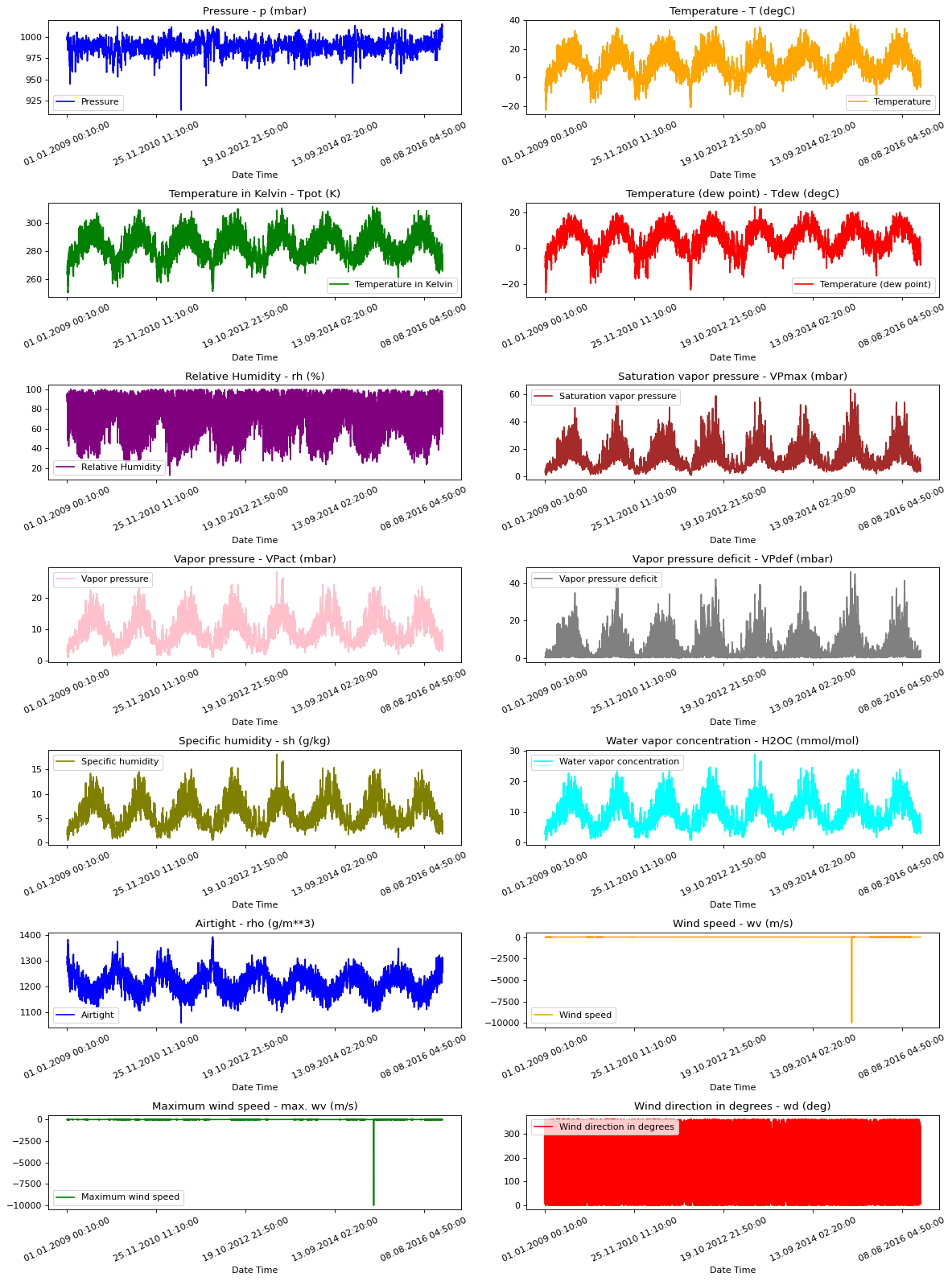
原始数据可视化
为了让我们了解正在处理的数据,以下绘制了每个特征。这显示了从 2009 年到 2016 年期间每个特征的独特模式。它还显示了异常值的位置,这些异常值将在后续的标准化过程中进行处理。
titles = [
"Pressure",
"Temperature",
"Temperature in Kelvin",
"Temperature (dew point)",
"Relative Humidity",
"Saturation vapor pressure",
"Vapor pressure",
"Vapor pressure deficit",
"Specific humidity",
"Water vapor concentration",
"Airtight",
"Wind speed",
"Maximum wind speed",
"Wind direction in degrees",
]
feature_keys = [
"p (mbar)",
"T (degC)",
"Tpot (K)",
"Tdew (degC)",
"rh (%)",
"VPmax (mbar)",
"VPact (mbar)",
"VPdef (mbar)",
"sh (g/kg)",
"H2OC (mmol/mol)",
"rho (g/m**3)",
"wv (m/s)",
"max. wv (m/s)",
"wd (deg)",
]
colors = [
"blue",
"orange",
"green",
"red",
"purple",
"brown",
"pink",
"gray",
"olive",
"cyan",
]
date_time_key = "Date Time"
def show_raw_visualization(data):
time_data = data[date_time_key]
fig, axes = plt.subplots(
nrows=7, ncols=2, figsize=(15, 20), dpi=80, facecolor="w", edgecolor="k"
)
for i in range(len(feature_keys)):
key = feature_keys[i]
c = colors[i % (len(colors))]
t_data = data[key]
t_data.index = time_data
t_data.head()
ax = t_data.plot(
ax=axes[i // 2, i % 2],
color=c,
title="{} - {}".format(titles[i], key),
rot=25,
)
ax.legend([titles[i]])
plt.tight_layout()
show_raw_visualization(df)
数据预处理
在这里,我们选取约 300,000 个数据点用于训练。观测每 10 分钟记录一次,即每小时 6 次。由于在 60 分钟内预计不会发生剧烈变化,我们将重采样为每小时一个点。我们通过 timeseries_dataset_from_array 工具中的 sampling_rate 参数来实现这一点。
我们跟踪过去 720 个时间戳(720/6=120 小时)的数据。这些数据将用于预测 72 个时间戳(72/6=12 小时)后的温度。
由于每个特征的值范围不同,我们在训练神经网络之前进行归一化,将特征值限制在 [0, 1] 的范围内。我们通过减去每个特征的均值并除以标准差来实现此目的。
71.5% 的数据将用于训练模型,即 300,693 行。可以通过更改 split_fraction 来改变此百分比。
模型将看到前 5 天的数据,即 720 个观测值,每小时采样一次。72 个观测值(12 小时 * 每小时 6 次观测)后的温度将用作标签。
split_fraction = 0.715
train_split = int(split_fraction * int(df.shape[0]))
step = 6
past = 720
future = 72
learning_rate = 0.001
batch_size = 256
epochs = 10
def normalize(data, train_split):
data_mean = data[:train_split].mean(axis=0)
data_std = data[:train_split].std(axis=0)
return (data - data_mean) / data_std
从相关性热图可以看出,相对湿度和比湿等几个参数是冗余的。因此,我们将使用部分特征,而不是全部。
print(
"The selected parameters are:",
", ".join([titles[i] for i in [0, 1, 5, 7, 8, 10, 11]]),
)
selected_features = [feature_keys[i] for i in [0, 1, 5, 7, 8, 10, 11]]
features = df[selected_features]
features.index = df[date_time_key]
features.head()
features = normalize(features.values, train_split)
features = pd.DataFrame(features)
features.head()
train_data = features.loc[0 : train_split - 1]
val_data = features.loc[train_split:]
The selected parameters are: Pressure, Temperature, Saturation vapor pressure, Vapor pressure deficit, Specific humidity, Airtight, Wind speed
训练数据集
训练数据集的标签从第 792 个观测值(720 + 72)开始。
start = past + future
end = start + train_split
x_train = train_data[[i for i in range(7)]].values
y_train = features.iloc[start:end][[1]]
sequence_length = int(past / step)
timeseries_dataset_from_array 函数接收一系列等间隔收集的数据点,以及时间序列参数,如序列/窗口的长度、序列/窗口之间的间隔等,以生成从主时间序列采样的子时间序列输入和目标批次。
dataset_train = keras.preprocessing.timeseries_dataset_from_array(
x_train,
y_train,
sequence_length=sequence_length,
sampling_rate=step,
batch_size=batch_size,
)
验证数据集
验证数据集不能包含最后 792 行,因为我们没有这些记录的标签数据,因此必须从数据末尾减去 792。
验证标签数据集必须从 train_split 之后的 792 开始,因此我们必须在 label_start 中加上 past + future (792)。
x_end = len(val_data) - past - future
label_start = train_split + past + future
x_val = val_data.iloc[:x_end][[i for i in range(7)]].values
y_val = features.iloc[label_start:][[1]]
dataset_val = keras.preprocessing.timeseries_dataset_from_array(
x_val,
y_val,
sequence_length=sequence_length,
sampling_rate=step,
batch_size=batch_size,
)
for batch in dataset_train.take(1):
inputs, targets = batch
print("Input shape:", inputs.numpy().shape)
print("Target shape:", targets.numpy().shape)
Input shape: (256, 120, 7)
Target shape: (256, 1)
训练
inputs = keras.layers.Input(shape=(inputs.shape[1], inputs.shape[2]))
lstm_out = keras.layers.LSTM(32)(inputs)
outputs = keras.layers.Dense(1)(lstm_out)
model = keras.Model(inputs=inputs, outputs=outputs)
model.compile(optimizer=keras.optimizers.Adam(learning_rate=learning_rate), loss="mse")
model.summary()
CUDA backend failed to initialize: Found cuSOLVER version 11405, but JAX was built against version 11502, which is newer. The copy of cuSOLVER that is installed must be at least as new as the version against which JAX was built. (Set TF_CPP_MIN_LOG_LEVEL=0 and rerun for more info.)
Model: "functional_1"
┏━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━┓ ┃ Layer (type) ┃ Output Shape ┃ Param # ┃ ┡━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━┩ │ input_layer (InputLayer) │ (None, 120, 7) │ 0 │ ├─────────────────────────────────┼───────────────────────────┼────────────┤ │ lstm (LSTM) │ (None, 32) │ 5,120 │ ├─────────────────────────────────┼───────────────────────────┼────────────┤ │ dense (Dense) │ (None, 1) │ 33 │ └─────────────────────────────────┴───────────────────────────┴────────────┘
Total params: 5,153 (20.13 KB)
Trainable params: 5,153 (20.13 KB)
Non-trainable params: 0 (0.00 B)
我们将使用 ModelCheckpoint 回调函数定期保存检查点,并使用 EarlyStopping 回调函数在验证损失不再改进时中断训练。
path_checkpoint = "model_checkpoint.weights.h5"
es_callback = keras.callbacks.EarlyStopping(monitor="val_loss", min_delta=0, patience=5)
modelckpt_callback = keras.callbacks.ModelCheckpoint(
monitor="val_loss",
filepath=path_checkpoint,
verbose=1,
save_weights_only=True,
save_best_only=True,
)
history = model.fit(
dataset_train,
epochs=epochs,
validation_data=dataset_val,
callbacks=[es_callback, modelckpt_callback],
)
Epoch 1/10
1172/1172 ━━━━━━━━━━━━━━━━━━━━ 0s 70ms/step - loss: 0.3008
Epoch 1: val_loss improved from inf to 0.15039, saving model to model_checkpoint.weights.h5
1172/1172 ━━━━━━━━━━━━━━━━━━━━ 104s 88ms/step - loss: 0.3007 - val_loss: 0.1504
Epoch 2/10
1171/1172 ━━━━━━━━━━━━━━━━━━━[37m━ 0s 66ms/step - loss: 0.1397
Epoch 2: val_loss improved from 0.15039 to 0.14231, saving model to model_checkpoint.weights.h5
1172/1172 ━━━━━━━━━━━━━━━━━━━━ 97s 83ms/step - loss: 0.1396 - val_loss: 0.1423
Epoch 3/10
1171/1172 ━━━━━━━━━━━━━━━━━━━[37m━ 0s 69ms/step - loss: 0.1242
Epoch 3: val_loss did not improve from 0.14231
1172/1172 ━━━━━━━━━━━━━━━━━━━━ 101s 86ms/step - loss: 0.1242 - val_loss: 0.1513
Epoch 4/10
1172/1172 ━━━━━━━━━━━━━━━━━━━━ 0s 68ms/step - loss: 0.1182
Epoch 4: val_loss did not improve from 0.14231
1172/1172 ━━━━━━━━━━━━━━━━━━━━ 102s 87ms/step - loss: 0.1182 - val_loss: 0.1503
Epoch 5/10
1171/1172 ━━━━━━━━━━━━━━━━━━━[37m━ 0s 67ms/step - loss: 0.1160
Epoch 5: val_loss did not improve from 0.14231
1172/1172 ━━━━━━━━━━━━━━━━━━━━ 100s 85ms/step - loss: 0.1160 - val_loss: 0.1500
Epoch 6/10
1171/1172 ━━━━━━━━━━━━━━━━━━━[37m━ 0s 69ms/step - loss: 0.1130
Epoch 6: val_loss did not improve from 0.14231
1172/1172 ━━━━━━━━━━━━━━━━━━━━ 100s 86ms/step - loss: 0.1130 - val_loss: 0.1469
Epoch 7/10
1172/1172 ━━━━━━━━━━━━━━━━━━━━ 0s 70ms/step - loss: 0.1106
Epoch 7: val_loss improved from 0.14231 to 0.13916, saving model to model_checkpoint.weights.h5
1172/1172 ━━━━━━━━━━━━━━━━━━━━ 104s 89ms/step - loss: 0.1106 - val_loss: 0.1392
Epoch 8/10
1171/1172 ━━━━━━━━━━━━━━━━━━━[37m━ 0s 66ms/step - loss: 0.1097
Epoch 8: val_loss improved from 0.13916 to 0.13257, saving model to model_checkpoint.weights.h5
1172/1172 ━━━━━━━━━━━━━━━━━━━━ 98s 84ms/step - loss: 0.1097 - val_loss: 0.1326
Epoch 9/10
1171/1172 ━━━━━━━━━━━━━━━━━━━[37m━ 0s 68ms/step - loss: 0.1075
Epoch 9: val_loss improved from 0.13257 to 0.13057, saving model to model_checkpoint.weights.h5
1172/1172 ━━━━━━━━━━━━━━━━━━━━ 100s 85ms/step - loss: 0.1075 - val_loss: 0.1306
Epoch 10/10
1172/1172 ━━━━━━━━━━━━━━━━━━━━ 0s 66ms/step - loss: 0.1065
Epoch 10: val_loss improved from 0.13057 to 0.12671, saving model to model_checkpoint.weights.h5
1172/1172 ━━━━━━━━━━━━━━━━━━━━ 98s 84ms/step - loss: 0.1065 - val_loss: 0.1267
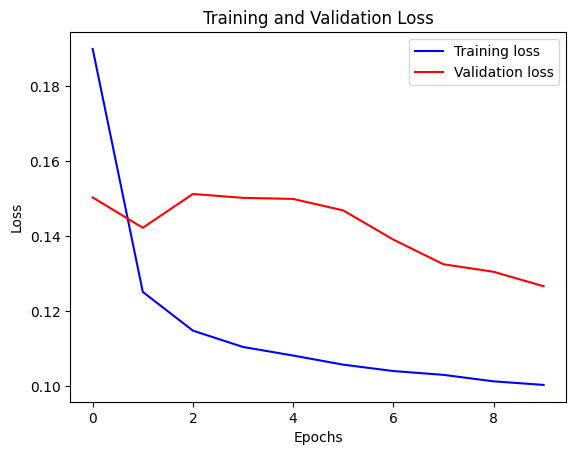
我们可以使用下面的函数可视化损失。一点之后,损失就不再下降了。
def visualize_loss(history, title):
loss = history.history["loss"]
val_loss = history.history["val_loss"]
epochs = range(len(loss))
plt.figure()
plt.plot(epochs, loss, "b", label="Training loss")
plt.plot(epochs, val_loss, "r", label="Validation loss")
plt.title(title)
plt.xlabel("Epochs")
plt.ylabel("Loss")
plt.legend()
plt.show()
visualize_loss(history, "Training and Validation Loss")
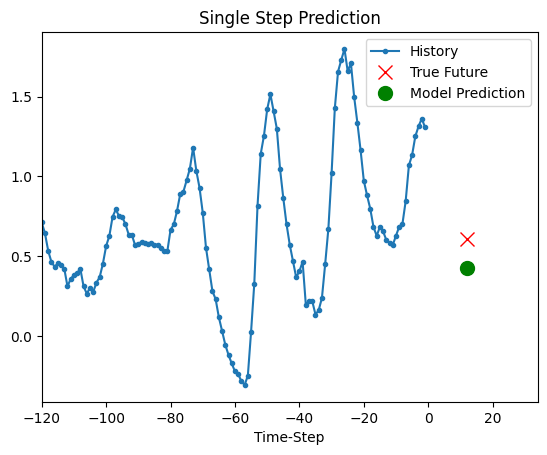
预测
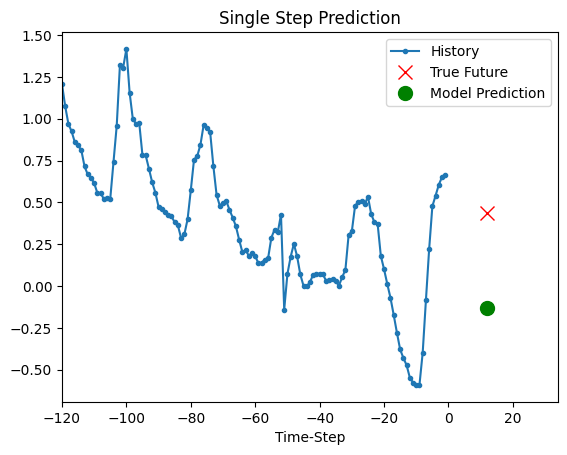
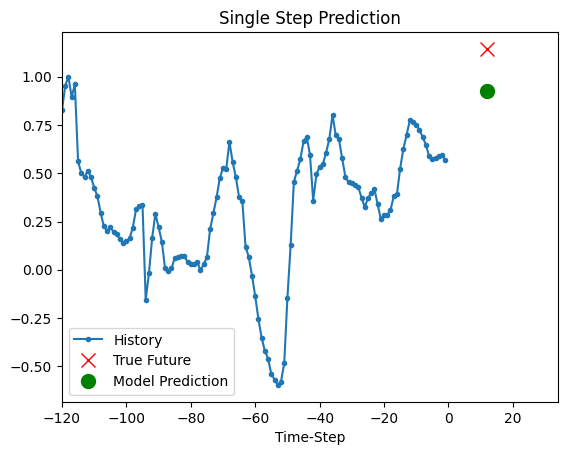
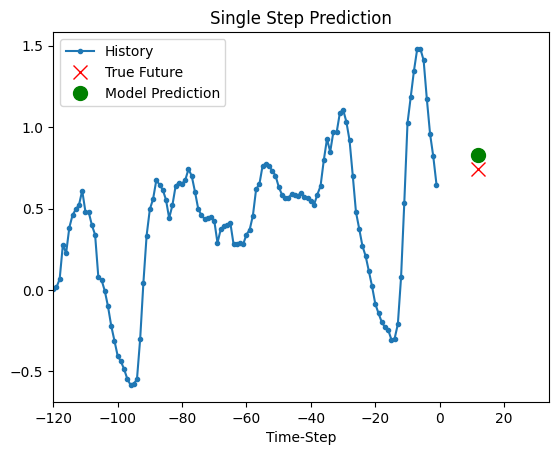
上面训练好的模型现在可以对验证集中的 5 组值进行预测。
def show_plot(plot_data, delta, title):
labels = ["History", "True Future", "Model Prediction"]
marker = [".-", "rx", "go"]
time_steps = list(range(-(plot_data[0].shape[0]), 0))
if delta:
future = delta
else:
future = 0
plt.title(title)
for i, val in enumerate(plot_data):
if i:
plt.plot(future, plot_data[i], marker[i], markersize=10, label=labels[i])
else:
plt.plot(time_steps, plot_data[i].flatten(), marker[i], label=labels[i])
plt.legend()
plt.xlim([time_steps[0], (future + 5) * 2])
plt.xlabel("Time-Step")
plt.show()
return
for x, y in dataset_val.take(5):
show_plot(
[x[0][:, 1].numpy(), y[0].numpy(), model.predict(x)[0]],
12,
"Single Step Prediction",
)
8/8 ━━━━━━━━━━━━━━━━━━━━ 0s 4ms/step
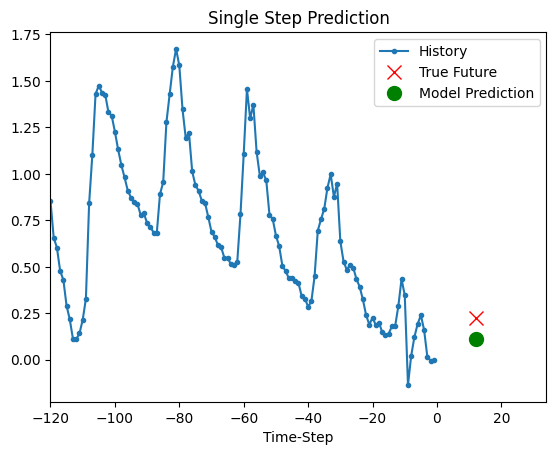
8/8 ━━━━━━━━━━━━━━━━━━━━ 0s 4ms/step
8/8 ━━━━━━━━━━━━━━━━━━━━ 0s 5ms/step
8/8 ━━━━━━━━━━━━━━━━━━━━ 0s 5ms/step
8/8 ━━━━━━━━━━━━━━━━━━━━ 0s 4ms/step