使用自动编码器进行时间序列异常检测
作者: pavithrasv
创建日期 2020/05/31
最后修改日期 2020/05/31
描述: 使用 Autoencoder 检测时间序列中的异常。
简介
此脚本演示了如何使用重建卷积自编码器模型来检测时间序列数据中的异常。
设置
import numpy as np
import pandas as pd
import keras
from keras import layers
from matplotlib import pyplot as plt
加载数据
我们将使用 Numenta 异常基准 (NAB) 数据集。它提供包含已标记的异常行为周期的人工时间序列数据。数据是按时间顺序排列的,带有时间戳,是单值指标。
我们将使用 art_daily_small_noise.csv 文件进行训练,并使用 art_daily_jumpsup.csv 文件进行测试。该数据集的简洁性使我们能够有效地演示异常检测。
master_url_root = "https://raw.githubusercontent.com/numenta/NAB/master/data/"
df_small_noise_url_suffix = "artificialNoAnomaly/art_daily_small_noise.csv"
df_small_noise_url = master_url_root + df_small_noise_url_suffix
df_small_noise = pd.read_csv(
df_small_noise_url, parse_dates=True, index_col="timestamp"
)
df_daily_jumpsup_url_suffix = "artificialWithAnomaly/art_daily_jumpsup.csv"
df_daily_jumpsup_url = master_url_root + df_daily_jumpsup_url_suffix
df_daily_jumpsup = pd.read_csv(
df_daily_jumpsup_url, parse_dates=True, index_col="timestamp"
)
快速查看数据
print(df_small_noise.head())
print(df_daily_jumpsup.head())
value
timestamp
2014-04-01 00:00:00 18.324919
2014-04-01 00:05:00 21.970327
2014-04-01 00:10:00 18.624806
2014-04-01 00:15:00 21.953684
2014-04-01 00:20:00 21.909120
value
timestamp
2014-04-01 00:00:00 19.761252
2014-04-01 00:05:00 20.500833
2014-04-01 00:10:00 19.961641
2014-04-01 00:15:00 21.490266
2014-04-01 00:20:00 20.187739
可视化数据
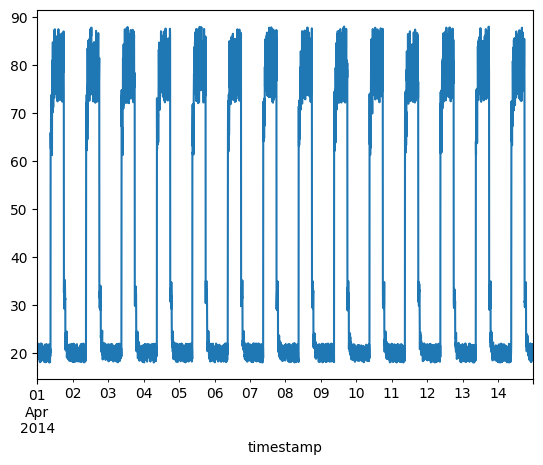
不含异常的时间序列数据
我们将使用以下数据进行训练。
fig, ax = plt.subplots()
df_small_noise.plot(legend=False, ax=ax)
plt.show()
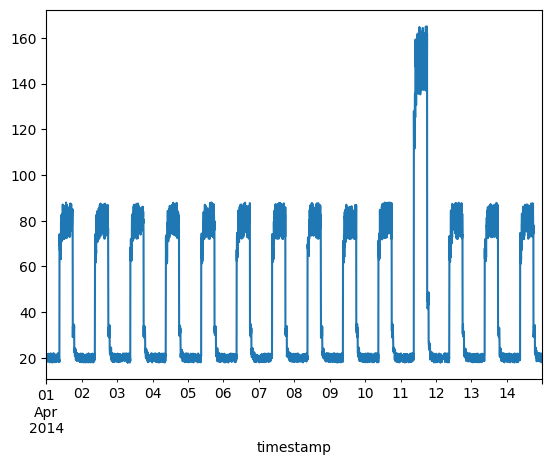
包含异常的时间序列数据
我们将使用以下数据进行测试,并查看数据中的突然跳升是否被检测为异常。
fig, ax = plt.subplots()
df_daily_jumpsup.plot(legend=False, ax=ax)
plt.show()
准备训练数据
从训练时间序列数据文件中获取数据值,并对 value 数据进行归一化。我们每 5 分钟有一个 value,持续 14 天。
- 24 * 60 / 5 = 每天 288 个时间步
- 288 * 14 = 总计 **4032 个数据点**
# Normalize and save the mean and std we get,
# for normalizing test data.
training_mean = df_small_noise.mean()
training_std = df_small_noise.std()
df_training_value = (df_small_noise - training_mean) / training_std
print("Number of training samples:", len(df_training_value))
Number of training samples: 4032
创建序列
通过组合训练数据中 TIME_STEPS 个连续的数据值来创建序列。
TIME_STEPS = 288
# Generated training sequences for use in the model.
def create_sequences(values, time_steps=TIME_STEPS):
output = []
for i in range(len(values) - time_steps + 1):
output.append(values[i : (i + time_steps)])
return np.stack(output)
x_train = create_sequences(df_training_value.values)
print("Training input shape: ", x_train.shape)
Training input shape: (3745, 288, 1)
构建一个模型
我们将构建一个卷积重建自编码器模型。该模型将接受形状为 (batch_size, sequence_length, num_features) 的输入,并返回相同形状的输出。在这种情况下,sequence_length 为 288,num_features 为 1。
model = keras.Sequential(
[
layers.Input(shape=(x_train.shape[1], x_train.shape[2])),
layers.Conv1D(
filters=32,
kernel_size=7,
padding="same",
strides=2,
activation="relu",
),
layers.Dropout(rate=0.2),
layers.Conv1D(
filters=16,
kernel_size=7,
padding="same",
strides=2,
activation="relu",
),
layers.Conv1DTranspose(
filters=16,
kernel_size=7,
padding="same",
strides=2,
activation="relu",
),
layers.Dropout(rate=0.2),
layers.Conv1DTranspose(
filters=32,
kernel_size=7,
padding="same",
strides=2,
activation="relu",
),
layers.Conv1DTranspose(filters=1, kernel_size=7, padding="same"),
]
)
model.compile(optimizer=keras.optimizers.Adam(learning_rate=0.001), loss="mse")
model.summary()
Model: "sequential"
┏━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━┓ ┃ Layer (type) ┃ Output Shape ┃ Param # ┃ ┡━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━┩ │ conv1d (Conv1D) │ (None, 144, 32) │ 256 │ ├─────────────────────────────────┼───────────────────────────┼────────────┤ │ dropout (Dropout) │ (None, 144, 32) │ 0 │ ├─────────────────────────────────┼───────────────────────────┼────────────┤ │ conv1d_1 (Conv1D) │ (None, 72, 16) │ 3,600 │ ├─────────────────────────────────┼───────────────────────────┼────────────┤ │ conv1d_transpose │ (None, 144, 16) │ 1,808 │ │ (Conv1DTranspose) │ │ │ ├─────────────────────────────────┼───────────────────────────┼────────────┤ │ dropout_1 (Dropout) │ (None, 144, 16) │ 0 │ ├─────────────────────────────────┼───────────────────────────┼────────────┤ │ conv1d_transpose_1 │ (None, 288, 32) │ 3,616 │ │ (Conv1DTranspose) │ │ │ ├─────────────────────────────────┼───────────────────────────┼────────────┤ │ conv1d_transpose_2 │ (None, 288, 1) │ 225 │ │ (Conv1DTranspose) │ │ │ └─────────────────────────────────┴───────────────────────────┴────────────┘
Total params: 9,505 (37.13 KB)
Trainable params: 9,505 (37.13 KB)
Non-trainable params: 0 (0.00 B)
训练模型
请注意,我们将 x_train 同时用作输入和目标,因为这是一个重建模型。
history = model.fit(
x_train,
x_train,
epochs=50,
batch_size=128,
validation_split=0.1,
callbacks=[
keras.callbacks.EarlyStopping(monitor="val_loss", patience=5, mode="min")
],
)
Epoch 1/50
26/27 ━━━━━━━━━━━━━━━━━━━[37m━ 0s 4ms/step - loss: 0.8419
WARNING: All log messages before absl::InitializeLog() is called are written to STDERR
I0000 00:00:1700346169.474466 1961179 device_compiler.h:187] Compiled cluster using XLA! This line is logged at most once for the lifetime of the process.
27/27 ━━━━━━━━━━━━━━━━━━━━ 10s 187ms/step - loss: 0.8262 - val_loss: 0.2280
Epoch 2/50
27/27 ━━━━━━━━━━━━━━━━━━━━ 0s 5ms/step - loss: 0.1485 - val_loss: 0.0513
Epoch 3/50
27/27 ━━━━━━━━━━━━━━━━━━━━ 0s 5ms/step - loss: 0.0659 - val_loss: 0.0389
Epoch 4/50
27/27 ━━━━━━━━━━━━━━━━━━━━ 0s 5ms/step - loss: 0.0563 - val_loss: 0.0341
Epoch 5/50
27/27 ━━━━━━━━━━━━━━━━━━━━ 0s 5ms/step - loss: 0.0489 - val_loss: 0.0298
Epoch 6/50
27/27 ━━━━━━━━━━━━━━━━━━━━ 0s 5ms/step - loss: 0.0434 - val_loss: 0.0272
Epoch 7/50
27/27 ━━━━━━━━━━━━━━━━━━━━ 0s 5ms/step - loss: 0.0386 - val_loss: 0.0258
Epoch 8/50
27/27 ━━━━━━━━━━━━━━━━━━━━ 0s 5ms/step - loss: 0.0349 - val_loss: 0.0241
Epoch 9/50
27/27 ━━━━━━━━━━━━━━━━━━━━ 0s 5ms/step - loss: 0.0319 - val_loss: 0.0230
Epoch 10/50
27/27 ━━━━━━━━━━━━━━━━━━━━ 0s 5ms/step - loss: 0.0297 - val_loss: 0.0236
Epoch 11/50
27/27 ━━━━━━━━━━━━━━━━━━━━ 0s 5ms/step - loss: 0.0279 - val_loss: 0.0233
Epoch 12/50
27/27 ━━━━━━━━━━━━━━━━━━━━ 0s 5ms/step - loss: 0.0264 - val_loss: 0.0225
Epoch 13/50
27/27 ━━━━━━━━━━━━━━━━━━━━ 0s 5ms/step - loss: 0.0255 - val_loss: 0.0228
Epoch 14/50
27/27 ━━━━━━━━━━━━━━━━━━━━ 0s 5ms/step - loss: 0.0245 - val_loss: 0.0223
Epoch 15/50
27/27 ━━━━━━━━━━━━━━━━━━━━ 0s 5ms/step - loss: 0.0236 - val_loss: 0.0234
Epoch 16/50
27/27 ━━━━━━━━━━━━━━━━━━━━ 0s 5ms/step - loss: 0.0227 - val_loss: 0.0256
Epoch 17/50
27/27 ━━━━━━━━━━━━━━━━━━━━ 0s 5ms/step - loss: 0.0219 - val_loss: 0.0240
Epoch 18/50
27/27 ━━━━━━━━━━━━━━━━━━━━ 0s 5ms/step - loss: 0.0214 - val_loss: 0.0245
Epoch 19/50
27/27 ━━━━━━━━━━━━━━━━━━━━ 0s 5ms/step - loss: 0.0207 - val_loss: 0.0250
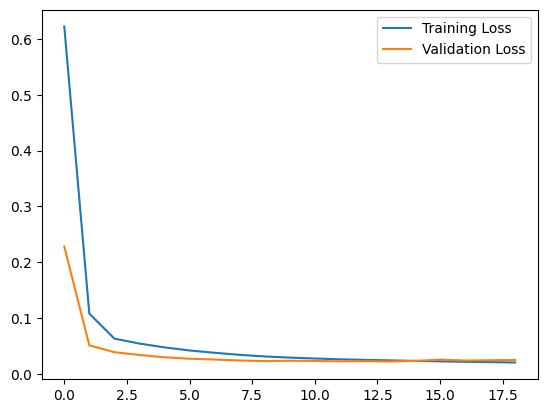
让我们绘制训练和验证损失图,看看训练效果如何。
plt.plot(history.history["loss"], label="Training Loss")
plt.plot(history.history["val_loss"], label="Validation Loss")
plt.legend()
plt.show()
检测异常
我们将通过确定模型能够多好地重建输入数据来检测异常。
- 在训练样本上查找 MAE 损失。
- 查找最大 MAE 损失值。这是模型在尝试重建样本时表现最差的情况。我们将此作为异常检测的
threshold。 - 如果样本的重建损失大于此
threshold值,那么我们可以推断模型看到的是一个它不熟悉的模式。我们将此样本标记为anomaly。
# Get train MAE loss.
x_train_pred = model.predict(x_train)
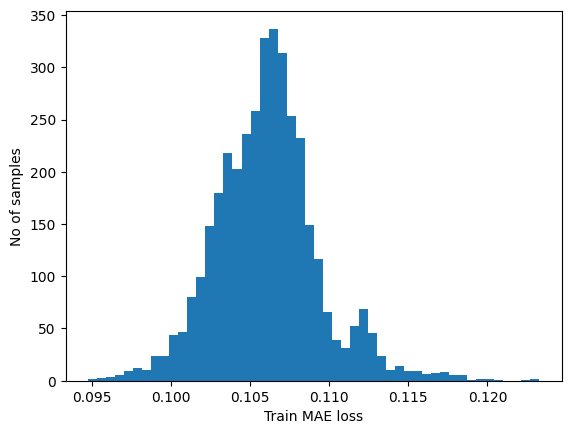
train_mae_loss = np.mean(np.abs(x_train_pred - x_train), axis=1)
plt.hist(train_mae_loss, bins=50)
plt.xlabel("Train MAE loss")
plt.ylabel("No of samples")
plt.show()
# Get reconstruction loss threshold.
threshold = np.max(train_mae_loss)
print("Reconstruction error threshold: ", threshold)
118/118 ━━━━━━━━━━━━━━━━━━━━ 1s 6ms/step
Reconstruction error threshold: 0.1232659916089631
比较重建
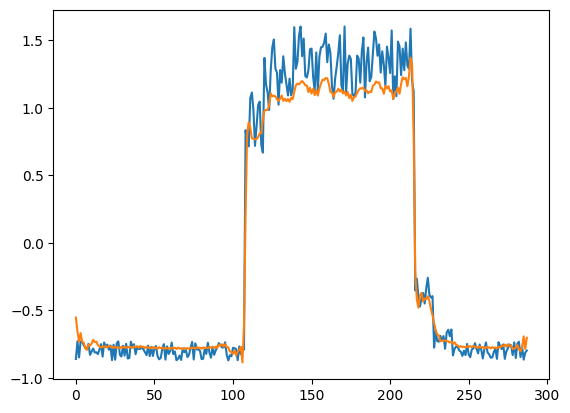
为了好玩,让我们看看我们的模型如何重建第一个样本。这是我们训练数据集第一天的 288 个时间步。
# Checking how the first sequence is learnt
plt.plot(x_train[0])
plt.plot(x_train_pred[0])
plt.show()
准备测试数据
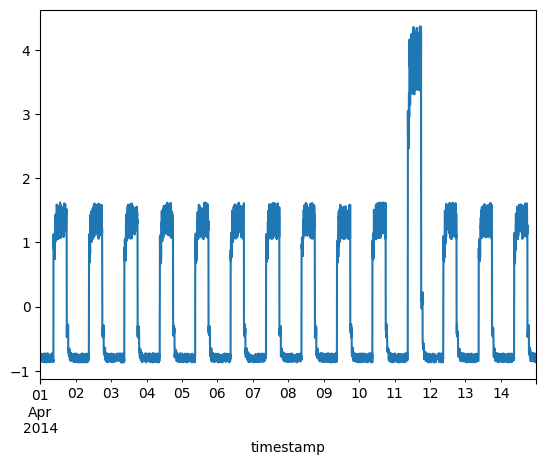
df_test_value = (df_daily_jumpsup - training_mean) / training_std
fig, ax = plt.subplots()
df_test_value.plot(legend=False, ax=ax)
plt.show()
# Create sequences from test values.
x_test = create_sequences(df_test_value.values)
print("Test input shape: ", x_test.shape)
# Get test MAE loss.
x_test_pred = model.predict(x_test)
test_mae_loss = np.mean(np.abs(x_test_pred - x_test), axis=1)
test_mae_loss = test_mae_loss.reshape((-1))
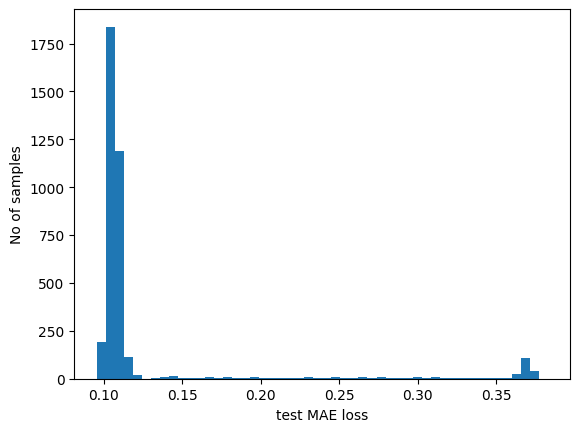
plt.hist(test_mae_loss, bins=50)
plt.xlabel("test MAE loss")
plt.ylabel("No of samples")
plt.show()
# Detect all the samples which are anomalies.
anomalies = test_mae_loss > threshold
print("Number of anomaly samples: ", np.sum(anomalies))
print("Indices of anomaly samples: ", np.where(anomalies))
Test input shape: (3745, 288, 1)
118/118 ━━━━━━━━━━━━━━━━━━━━ 0s 1ms/step
Number of anomaly samples: 394
Indices of anomaly samples: (array([1654, 2702, 2703, 2704, 2705, 2706, 2707, 2708, 2709, 2710, 2711,
2712, 2713, 2714, 2715, 2716, 2717, 2718, 2719, 2720, 2721, 2722,
2723, 2724, 2725, 2726, 2727, 2728, 2729, 2730, 2731, 2732, 2733,
2734, 2735, 2736, 2737, 2738, 2739, 2740, 2741, 2742, 2743, 2744,
2745, 2746, 2747, 2748, 2749, 2750, 2751, 2752, 2753, 2754, 2755,
2756, 2757, 2758, 2759, 2760, 2761, 2762, 2763, 2764, 2765, 2766,
2767, 2768, 2769, 2770, 2771, 2772, 2773, 2774, 2775, 2776, 2777,
2778, 2779, 2780, 2781, 2782, 2783, 2784, 2785, 2786, 2787, 2788,
2789, 2790, 2791, 2792, 2793, 2794, 2795, 2796, 2797, 2798, 2799,
2800, 2801, 2802, 2803, 2804, 2805, 2806, 2807, 2808, 2809, 2810,
2811, 2812, 2813, 2814, 2815, 2816, 2817, 2818, 2819, 2820, 2821,
2822, 2823, 2824, 2825, 2826, 2827, 2828, 2829, 2830, 2831, 2832,
2833, 2834, 2835, 2836, 2837, 2838, 2839, 2840, 2841, 2842, 2843,
2844, 2845, 2846, 2847, 2848, 2849, 2850, 2851, 2852, 2853, 2854,
2855, 2856, 2857, 2858, 2859, 2860, 2861, 2862, 2863, 2864, 2865,
2866, 2867, 2868, 2869, 2870, 2871, 2872, 2873, 2874, 2875, 2876,
2877, 2878, 2879, 2880, 2881, 2882, 2883, 2884, 2885, 2886, 2887,
2888, 2889, 2890, 2891, 2892, 2893, 2894, 2895, 2896, 2897, 2898,
2899, 2900, 2901, 2902, 2903, 2904, 2905, 2906, 2907, 2908, 2909,
2910, 2911, 2912, 2913, 2914, 2915, 2916, 2917, 2918, 2919, 2920,
2921, 2922, 2923, 2924, 2925, 2926, 2927, 2928, 2929, 2930, 2931,
2932, 2933, 2934, 2935, 2936, 2937, 2938, 2939, 2940, 2941, 2942,
2943, 2944, 2945, 2946, 2947, 2948, 2949, 2950, 2951, 2952, 2953,
2954, 2955, 2956, 2957, 2958, 2959, 2960, 2961, 2962, 2963, 2964,
2965, 2966, 2967, 2968, 2969, 2970, 2971, 2972, 2973, 2974, 2975,
2976, 2977, 2978, 2979, 2980, 2981, 2982, 2983, 2984, 2985, 2986,
2987, 2988, 2989, 2990, 2991, 2992, 2993, 2994, 2995, 2996, 2997,
2998, 2999, 3000, 3001, 3002, 3003, 3004, 3005, 3006, 3007, 3008,
3009, 3010, 3011, 3012, 3013, 3014, 3015, 3016, 3017, 3018, 3019,
3020, 3021, 3022, 3023, 3024, 3025, 3026, 3027, 3028, 3029, 3030,
3031, 3032, 3033, 3034, 3035, 3036, 3037, 3038, 3039, 3040, 3041,
3042, 3043, 3044, 3045, 3046, 3047, 3048, 3049, 3050, 3051, 3052,
3053, 3054, 3055, 3056, 3057, 3058, 3059, 3060, 3061, 3062, 3063,
3064, 3065, 3066, 3067, 3068, 3069, 3070, 3071, 3072, 3073, 3074,
3075, 3076, 3077, 3078, 3079, 3080, 3081, 3082, 3083, 3084, 3085,
3086, 3087, 3088, 3089, 3090, 3091, 3092, 3093, 3094]),)
绘制异常
我们现在知道数据中哪些样本是异常的。有了这个,我们将从原始测试数据中找到对应的 timestamps。我们将使用以下方法来做到这一点
假设 time_steps = 3,我们有 10 个训练值。我们的 x_train 将如下所示
- 0, 1, 2
- 1, 2, 3
- 2, 3, 4
- 3, 4, 5
- 4, 5, 6
- 5, 6, 7
- 6, 7, 8
- 7, 8, 9
除了初始和最后的 time_steps-1 个数据值之外的所有值,都将出现在 time_steps 个样本中。因此,如果我们知道样本 [(3, 4, 5), (4, 5, 6), (5, 6, 7)] 是异常的,我们可以说数据点 5 是一个异常。
# data i is an anomaly if samples [(i - timesteps + 1) to (i)] are anomalies
anomalous_data_indices = []
for data_idx in range(TIME_STEPS - 1, len(df_test_value) - TIME_STEPS + 1):
if np.all(anomalies[data_idx - TIME_STEPS + 1 : data_idx]):
anomalous_data_indices.append(data_idx)
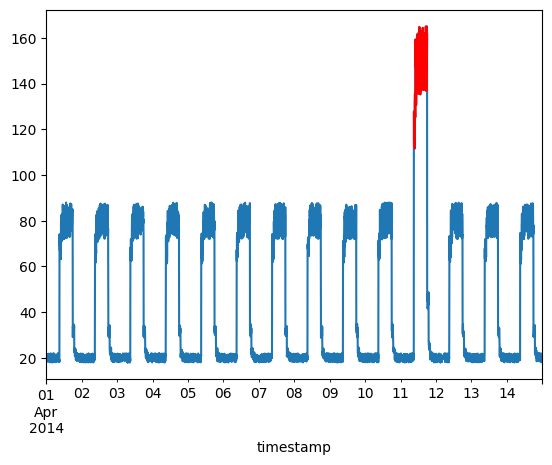
让我们将异常叠加到原始测试数据图上。
df_subset = df_daily_jumpsup.iloc[anomalous_data_indices]
fig, ax = plt.subplots()
df_daily_jumpsup.plot(legend=False, ax=ax)
df_subset.plot(legend=False, ax=ax, color="r")
plt.show()