深度推荐系统
作者: Fabien Hertschuh, Abheesht Sharma
创建日期 2025/04/28
最后修改日期 2025/04/28
描述: 使用多个堆叠层构建深度检索模型。
简介
使用 Keras 构建推荐模型的一大优势在于可以自由构建丰富、灵活的特征表示。
这样做的第一步是准备特征,因为原始特征通常不能直接在模型中使用。
例如
- 用户和物品 ID 可能是字符串(标题、用户名)或大型、不连续的整数(数据库 ID)。
- 物品描述可以是原始文本。
- 交互时间戳可以是原始 Unix 时间戳。
这些需要经过适当的转换才能在构建模型时发挥作用。
- 用户和物品 ID 必须转换为嵌入向量,这些高维数值表示在训练过程中进行调整,以帮助模型更好地预测其目标。
- 原始文本需要进行分词(拆分成更小的部分,如单个单词)并转换为嵌入。
- 数值特征需要进行归一化,使其值落在 0 附近的一个小区间内。
幸运的是,Keras 的 FeatureSpace 工具可以轻松完成此预处理。
在本教程中,我们将把多个特征整合到我们的模型中。这些特征将来自 MovieLens 数据集的预处理。
在 基本检索 教程中,模型仅包含一个嵌入层。在本教程中,我们为模型添加了更多密集层,以增加其表达能力。
通常,更深的模型比浅层模型更能学习到复杂的模式。例如,我们的用户模型包含用户 ID 和用户特征,如年龄、性别和职业。浅层模型(例如,单个嵌入层)可能只能学习到这些特征与电影之间最简单的关系:某个用户通常更喜欢恐怖片而非喜剧片。要捕捉更复杂的关系,例如用户偏好会随着年龄而变化,我们可能需要一个具有多个堆叠密集层的更深层模型。
当然,复杂的模型也有其缺点。第一个是计算成本,因为更大的模型在训练和提供服务时都需要更多的内存和计算。第二个是需要更多的数据。通常,需要更多的训练数据才能利用更深层模型。具有更多参数的深度模型可能会过拟合,甚至简单地记住训练示例,而不是学习一个能够泛化的函数。最后,训练更深层模型可能更难,需要更仔细地选择正则化和学习率等设置。
为实际的推荐系统找到一个好的架构是一门复杂的艺术,需要良好的直觉和细致的超参数调优。例如,模型的深度和宽度、激活函数、学习率和优化器等因素会极大地改变模型的性能。建模选择因以下事实而进一步复杂化:良好的离线评估指标可能与良好的在线性能不对应,而且选择优化什么往往比选择模型本身更关键。
尽管如此,在构建和微调更大模型上付出的努力通常会得到回报。在本教程中,我们将演示如何构建一个深度检索模型。我们将通过构建越来越复杂的模型来查看这如何影响模型性能。
!pip install -q keras-rs
import os
os.environ["KERAS_BACKEND"] = "jax" # `"tensorflow"`/`"torch"`
import keras
import matplotlib.pyplot as plt
import tensorflow as tf # Needed for the dataset
import tensorflow_datasets as tfds
import keras_rs
MovieLens 数据集
首先,让我们看看 MovieLens 数据集中我们可以使用哪些特征。
# Ratings data with user and movie data.
ratings = tfds.load("movielens/100k-ratings", split="train")
# Features of all the available movies.
movies = tfds.load("movielens/100k-movies", split="train")
评分数据集返回一个字典,包含电影 ID、用户 ID、分配的评分、时间戳、电影信息和用户信息。
for data in ratings.take(1).as_numpy_iterator():
print(str(data).replace(", '", ",\n '"))
{'bucketized_user_age': np.float32(45.0),
'movie_genres': array([7]),
'movie_id': b'357',
'movie_title': b"One Flew Over the Cuckoo's Nest (1975)",
'raw_user_age': np.float32(46.0),
'timestamp': np.int64(879024327),
'user_gender': np.True_,
'user_id': b'138',
'user_occupation_label': np.int64(4),
'user_occupation_text': b'doctor',
'user_rating': np.float32(4.0),
'user_zip_code': b'53211'}
在 Movielens 数据集中,用户 ID 是从 1 开始且没有间隙的整数(表示为字符串)。通常,您需要创建一个查找表将用户 ID 映射到 0 到 N-1 的整数。但为了简化,我们将直接使用用户 ID 作为模型中的索引,特别是用于从用户嵌入表中查找用户嵌入。因此,我们需要知道用户的数量。
USERS_COUNT = (
ratings.map(lambda x: tf.strings.to_number(x["user_id"], out_type=tf.int32))
.reduce(tf.constant(0, tf.int32), tf.maximum)
.numpy()
)
电影数据集包含电影 ID、电影标题以及所属的类型。请注意,类型是用整数标签编码的。
for data in movies.take(1).as_numpy_iterator():
print(str(data).replace(", '", ",\n '"))
{'movie_genres': array([4]),
'movie_id': b'1681',
'movie_title': b'You So Crazy (1994)'}
在 Movielens 数据集中,电影 ID 是从 1 开始且没有间隙的整数(表示为字符串)。通常,您需要创建一个查找表将电影 ID 映射到 0 到 N-1 的整数。但为了简化,我们将直接使用电影 ID 作为模型中的索引,特别是用于从电影嵌入表中查找电影嵌入。因此,我们需要知道电影的数量。
MOVIES_COUNT = movies.cardinality().numpy()
预处理数据集
归一化连续特征
连续特征可能需要归一化,以便它们落在模型的可接受范围内。我们将举两个这样的归例。
离散化
一种常见的转换是将连续特征转换为多个分类特征。如果我们有理由怀疑某个特征的影响是非连续的,那么这样做是有意义的。
我们需要决定用于离散化的桶的数量。然后,我们将使用 Keras 的 FeatureSpace 工具自动查找最小值和最大值,并将该范围除以桶的数量以执行离散化。
在本例中,我们将对用户年龄进行离散化。
AGE_BINS_COUNT = 10
user_age_feature = keras.utils.FeatureSpace.float_discretized(
num_bins=AGE_BINS_COUNT, output_mode="int"
)
缩放
通常,我们希望连续特征介于 0 和 1 之间,或者介于 -1 和 1 之间。要实现这一点,我们可以对具有不同范围的特征进行重缩放。
在本例中,我们将对评分(一个介于 1 和 5 之间的整数)进行标准化,使其成为介于 0 和 1 之间的浮点数。我们需要对其进行重缩放并进行偏移。
user_rating_feature = keras.utils.FeatureSpace.float_rescaled(
scale=1.0 / 4.0, offset=-1.0 / 4.0
)
将分类特征转换为嵌入
分类特征是指不表示连续数量,而是取一组固定值之一的特征。
大多数深度学习模型通过将这些特征转换为高维向量来表示它们。在模型训练过程中,该向量的值会进行调整,以帮助模型更好地预测其目标。
例如,假设我们的目标是预测哪个用户将观看哪个电影。为此,我们用一个嵌入向量表示每个用户和每个电影。最初,这些嵌入将取随机值。在训练过程中,我们会调整它们,以便观看电影的用户和电影的嵌入最终靠得更近。
将原始分类特征转换为嵌入通常是一个两步过程:1. 首先,我们需要将原始值转换为一系列连续的整数,通常通过构建一个映射(称为“词汇表”)来将原始值映射到整数。2. 其次,我们需要将这些整数转换为嵌入。
定义分类特征
我们将使用 Keras 的 FeatureSpace 工具来完成第一步。它的 adapt 方法会自动发现分类特征的词汇表。
user_gender_feature = keras.utils.FeatureSpace.integer_categorical(
num_oov_indices=0, output_mode="int"
)
user_occupation_feature = keras.utils.FeatureSpace.integer_categorical(
num_oov_indices=0, output_mode="int"
)
使用特征交叉
通过交叉,我们可以实现多个分类特征之间的特征交互。这对于表达特征组合代表特定的电影品味非常有用。
请注意,多个特征的组合可能会导致一个非常大的特征空间,这就是为什么 crossing_dim 参数很重要,以限制交叉特征的输出维度。
在本例中,我们将使用 Keras 的 FeatureSpace 工具来交叉年龄和性别。
USER_GENDER_CROSS_COUNT = 20
user_gender_age_cross = keras.utils.FeatureSpace.cross(
feature_names=("user_gender", "raw_user_age"),
crossing_dim=USER_GENDER_CROSS_COUNT,
output_mode="int",
)
处理文本特征
我们也可能想在模型中添加文本特征。通常,产品描述等是自由格式文本,我们可以希望我们的模型能够利用它们包含的信息来做出更好的推荐,尤其是在冷启动或长尾场景下。
虽然 MovieLens 数据集没有提供丰富的文本特征,但我们仍然可以使用电影标题。这有助于我们捕捉标题非常相似的电影很可能属于同一系列的这一事实。
我们需要应用于文本的第一个转换是分词(拆分成构成单词或词片段),然后是词汇表学习,最后是嵌入。
[keras.layers.TextVectorization](/api/layers/preprocessing_layers/text/text_vectorization#textvectorization-class) 层可以为我们完成前两步。
title_vectorizer = keras.layers.TextVectorization(
max_tokens=10_000, output_sequence_length=16, dtype="int32"
)
title_vectorizer.adapt(movies.map(lambda x: x["movie_title"]))
让我们试试看
for data in movies.take(1).as_numpy_iterator():
print(title_vectorizer(data["movie_title"]))
[ 59 187 622 5 0 0 0 0 0 0 0 0 0 0 0 0]
每个标题都被转换为一个标记序列,每个标记代表我们分词的每个片段。
我们可以检查学习到的词汇表,以验证该层是否使用了正确的标记化
print(title_vectorizer.get_vocabulary()[40:50])
[np.str_('paris'), np.str_('little'), np.str_('last'), np.str_('ii'), np.str_('1988'), np.str_('king'), np.str_('from'), np.str_('city'), np.str_('boys'), np.str_('murder')]
这看起来是正确的,该层将标题分词为单个单词。稍后,我们将看到如何嵌入这些分词后的文本。现在,我们将这个分词器转换为 Keras FeatureSpace 特征。
title_feature = keras.utils.FeatureSpace.feature(
preprocessor=title_vectorizer, dtype="string", output_mode="float"
)
TITLE_TOKEN_COUNT = title_vectorizer.vocabulary_size()
将 FeatureSpace 特征组合在一起
现在我们准备好将具有预处理器的特征组合到一个 FeatureSpace 对象中。然后,我们使用 adapt 方法遍历数据集并学习需要学习的内容,例如分类特征的词汇表大小或分桶特征的最小值和最大值。
feature_space = keras.utils.FeatureSpace(
features={
# Numerical features to discretize.
"raw_user_age": user_age_feature,
# Categorical features encoded as integers.
"user_gender": user_gender_feature,
"user_occupation_label": user_occupation_feature,
# Labels are ratings between 0 and 1.
"user_rating": user_rating_feature,
"movie_title": title_feature,
},
crosses=[user_gender_age_cross],
output_mode="dict",
)
feature_space.adapt(ratings)
GENDERS_COUNT = feature_space.preprocessors["user_gender"].vocabulary_size()
OCCUPATIONS_COUNT = feature_space.preprocessors[
"user_occupation_label"
].vocabulary_size()
预构建候选集
我们的模型将基于 Retrieval 层,该层可以提供一组最佳候选项。为此,检索层需要了解所有候选项及其特征。在本节中,我们将电影的完整集合及其相关特征组合在一起。
提取原始候选特征
首先,我们将数据集中的所有原始特征收集到列表中。这些是电影的标题和类型。请注意,每部电影都关联有一个或多个类型,并且每部电影的类型数量各不相同。
movie_titles = [""] * (MOVIES_COUNT + 1)
movie_genres = [[]] * (MOVIES_COUNT + 1)
for x in movies.as_numpy_iterator():
movie_id = int(x["movie_id"])
movie_titles[movie_id] = x["movie_title"]
movie_genres[movie_id] = x["movie_genres"].tolist()
预处理候选特征
类型已经以从零开始的类别编号形式给出。但是,我们需要确定两件事:- 一部电影可以拥有的最大类型数量;这将决定该特征的维度。- 类别的最大值,这将给出总类别数量并确定我们用于类型的嵌入表的大小。
MAX_GENRES_PER_MOVIE = 0
max_genre_id = 0
for one_movie_genres in movie_genres:
MAX_GENRES_PER_MOVIE = max(MAX_GENRES_PER_MOVIE, len(one_movie_genres))
if one_movie_genres:
max_genre_id = max(max_genre_id, max(one_movie_genres))
GENRES_COUNT = max_genre_id + 1
现在我们需要用一个“未知”(Out Of Vocabulary)值来填充类型,以便能够将类型表示为固定大小的向量。为简单起见,我们将用零填充,因此我们将类型加 1,以避免与类型零冲突,因为类型零是一个有效的类型。
movie_genres = [
[g + 1 for g in genres] + [0] * (MAX_GENRES_PER_MOVIE - len(genres))
for genres in movie_genres
]
然后,我们对所有电影标题进行向量化。
movie_titles_vectors = title_vectorizer(movie_titles)
将候选集转换为原生张量
现在我们准备将这些内容组合到一个数据集中。最后一步是确保所有内容都是检索层可以消耗的原生张量。提醒一下,电影 ID 零不存在。
MOVIES_DATASET = {
"movie_id": keras.ops.arange(0, MOVIES_COUNT + 1, dtype="int32"),
"movie_title_vector": movie_titles_vectors,
"movie_genres": keras.ops.convert_to_tensor(movie_genres, dtype="int32"),
}
准备数据
我们现在可以定义我们的预处理函数。大多数特征将由 FeatureSpace 处理。需要提取用户 ID 和电影 ID。电影类型需要填充。然后所有内容都打包成一个元组,其中包含一个输入特征字典和一个用于评分(用作标签)的浮点数。
def preprocess_rating(x):
features = feature_space(
{
"raw_user_age": x["raw_user_age"],
"user_gender": x["user_gender"],
"user_occupation_label": x["user_occupation_label"],
"user_rating": x["user_rating"],
"movie_title": x["movie_title"],
}
)
features = {k: tf.squeeze(v, axis=0) for k, v in features.items()}
movie_genres = x["movie_genres"]
return (
{
# User inputs are user ID and user features
"user_id": int(x["user_id"]),
"raw_user_age": features["raw_user_age"],
"user_gender": features["user_gender"],
"user_occupation_label": features["user_occupation_label"],
"user_gender_X_raw_user_age": tf.squeeze(
features["user_gender_X_raw_user_age"], axis=-1
),
# Movie inputs are movie ID, vectorized title and genres
"movie_id": int(x["movie_id"]),
"movie_title_vector": features["movie_title"],
"movie_genres": tf.pad(
movie_genres + 1,
[[0, MAX_GENRES_PER_MOVIE - tf.shape(movie_genres)[0]]],
),
},
# Label is user rating between 0 and 1
features["user_rating"],
)
我们进行洗牌,然后将数据分成训练集和测试集。
shuffled_ratings = ratings.map(preprocess_rating).shuffle(
100_000, seed=42, reshuffle_each_iteration=False
)
train_ratings = shuffled_ratings.take(80_000).batch(1000).cache()
test_ratings = shuffled_ratings.skip(80_000).take(20_000).batch(1000).cache()
模型定义
查询模型
查询模型首先负责将用户特征转换为嵌入。然后将嵌入连接成一个单一向量。
定义更深层的模型需要我们在第一组嵌入之上堆叠更多层。通常的模式是使用一个由激活函数分隔的、逐渐变窄的层堆栈。
+----------------------+
| 64 x 32 |
+----------------------+
| relu
+--------------------------+
| 128 x 64 |
+--------------------------+
| relu
+------------------------------+
| ... x 128 |
+------------------------------+
由于深度线性模型的可表达能力不大于浅层线性模型,因此我们对除最后一层隐藏层之外的所有层都使用 ReLU 激活。最后一个隐藏层不使用任何激活函数:使用激活函数会限制最终嵌入的输出空间,并可能对模型的性能产生负面影响。例如,如果在投影层中使用 ReLU,则输出嵌入中的所有分量都将是非负的。
我们将在本次尝试。为了方便试验不同深度的模型,让我们定义一个其深度(和宽度)由构造函数参数确定的模型。layer_sizes 参数提供了模型的深度和宽度。我们可以更改它来尝试更浅或更深的模型。
class QueryModel(keras.Model):
"""Model for encoding user queries."""
def __init__(self, layer_sizes, embedding_dimension=32):
"""Construct a model for encoding user queries.
Args:
layer_sizes: A list of integers where the i-th entry represents the
number of units the i-th layer contains.
embedding_dimension: Output dimension for all embedding tables.
"""
super().__init__()
# We first generate embeddings.
self.user_embedding = keras.layers.Embedding(
# +1 for user ID zero, which does not exist
USERS_COUNT + 1,
embedding_dimension,
)
self.gender_embedding = keras.layers.Embedding(
GENDERS_COUNT, embedding_dimension
)
self.age_embedding = keras.layers.Embedding(AGE_BINS_COUNT, embedding_dimension)
self.gender_x_age_embedding = keras.layers.Embedding(
USER_GENDER_CROSS_COUNT, embedding_dimension
)
self.occupation_embedding = keras.layers.Embedding(
OCCUPATIONS_COUNT, embedding_dimension
)
# Then construct the layers.
self.dense_layers = keras.Sequential()
# Use the ReLU activation for all but the last layer.
for layer_size in layer_sizes[:-1]:
self.dense_layers.add(keras.layers.Dense(layer_size, activation="relu"))
# No activation for the last layer.
self.dense_layers.add(keras.layers.Dense(layer_sizes[-1]))
def call(self, inputs):
# Take the inputs, pass each through its embedding layer, concatenate.
feature_embedding = keras.ops.concatenate(
[
self.user_embedding(inputs["user_id"]),
self.gender_embedding(inputs["user_gender"]),
self.age_embedding(inputs["raw_user_age"]),
self.gender_x_age_embedding(inputs["user_gender_X_raw_user_age"]),
self.occupation_embedding(inputs["user_occupation_label"]),
],
axis=1,
)
return self.dense_layers(feature_embedding)
候选模型
我们可以对候选模型采用相同的方法。同样,我们首先将电影特征转换为嵌入,将它们连接起来,然后用隐藏层进行扩展。
class CandidateModel(keras.Model):
"""Model for encoding candidates (movies)."""
def __init__(self, layer_sizes, embedding_dimension=32):
"""Construct a model for encoding candidates (movies).
Args:
layer_sizes: A list of integers where the i-th entry represents the
number of units the i-th layer contains.
embedding_dimension: Output dimension for all embedding tables.
"""
super().__init__()
# We first generate embeddings.
self.movie_embedding = keras.layers.Embedding(
# +1 for movie ID zero, which does not exist
MOVIES_COUNT + 1,
embedding_dimension,
)
# Take all the title tokens for the title of the movie, embed each
# token, and then take the mean of all token embeddings.
self.movie_title_embedding = keras.Sequential(
[
keras.layers.Embedding(
# +1 for OOV token, which is used for padding
TITLE_TOKEN_COUNT + 1,
embedding_dimension,
mask_zero=True,
),
keras.layers.GlobalAveragePooling1D(),
]
)
# Take all the genres for the movie, embed each genre, and then take the
# mean of all genre embeddings.
self.movie_genres_embedding = keras.Sequential(
[
keras.layers.Embedding(
# +1 for OOV genre, which is used for padding
GENRES_COUNT + 1,
embedding_dimension,
mask_zero=True,
),
keras.layers.GlobalAveragePooling1D(),
]
)
# Then construct the layers.
self.dense_layers = keras.Sequential()
# Use the ReLU activation for all but the last layer.
for layer_size in layer_sizes[:-1]:
self.dense_layers.add(keras.layers.Dense(layer_size, activation="relu"))
# No activation for the last layer.
self.dense_layers.add(keras.layers.Dense(layer_sizes[-1]))
def call(self, inputs):
movie_id = inputs["movie_id"]
movie_title_vector = inputs["movie_title_vector"]
movie_genres = inputs["movie_genres"]
feature_embedding = keras.ops.concatenate(
[
self.movie_embedding(movie_id),
self.movie_title_embedding(movie_title_vector),
self.movie_genres_embedding(movie_genres),
],
axis=1,
)
return self.dense_layers(feature_embedding)
组合模型
定义了 QueryModel 和 CandidateModel 后,我们可以将它们组合成一个模型,并实现我们的损失和指标逻辑。为了简化,我们将强制查询模型和候选模型具有相同的结构。
class RetrievalModel(keras.Model):
"""Combined model."""
def __init__(
self,
layer_sizes=(32,),
embedding_dimension=32,
retrieval_k=100,
):
"""Construct a combined model.
Args:
layer_sizes: A list of integers where the i-th entry represents the
number of units the i-th layer contains.
embedding_dimension: Output dimension for all embedding tables.
retrieval_k: How many candidate movies to retrieve.
"""
super().__init__()
self.query_model = QueryModel(layer_sizes, embedding_dimension)
self.candidate_model = CandidateModel(layer_sizes, embedding_dimension)
self.retrieval = keras_rs.layers.BruteForceRetrieval(
k=retrieval_k, return_scores=False
)
self.update_candidates() # Provide an initial set of candidates
self.loss_fn = keras.losses.MeanSquaredError()
self.top_k_metric = keras.metrics.SparseTopKCategoricalAccuracy(
k=retrieval_k, from_sorted_ids=True
)
def update_candidates(self):
self.retrieval.update_candidates(
self.candidate_model.predict(MOVIES_DATASET, verbose=0)
)
def call(self, inputs, training=False):
query_embeddings = self.query_model(
{
"user_id": inputs["user_id"],
"raw_user_age": inputs["raw_user_age"],
"user_gender": inputs["user_gender"],
"user_occupation_label": inputs["user_occupation_label"],
"user_gender_X_raw_user_age": inputs["user_gender_X_raw_user_age"],
}
)
candidate_embeddings = self.candidate_model(
{
"movie_id": inputs["movie_id"],
"movie_title_vector": inputs["movie_title_vector"],
"movie_genres": inputs["movie_genres"],
}
)
result = {
"query_embeddings": query_embeddings,
"candidate_embeddings": candidate_embeddings,
}
if not training:
# No need to spend time extracting top predicted movies during
# training, they are not used.
result["predictions"] = self.retrieval(query_embeddings)
return result
def evaluate(
self,
x=None,
y=None,
batch_size=None,
verbose="auto",
sample_weight=None,
steps=None,
callbacks=None,
return_dict=False,
**kwargs,
):
"""Overridden to update the candidate set.
Before evaluating the model, we need to update our retrieval layer by
re-computing the values predicted by the candidate model for all the
candidates.
"""
self.update_candidates()
return super().evaluate(
x,
y,
batch_size=batch_size,
verbose=verbose,
sample_weight=sample_weight,
steps=steps,
callbacks=callbacks,
return_dict=return_dict,
**kwargs,
)
def compute_loss(self, x, y, y_pred, sample_weight, training=True):
query_embeddings = y_pred["query_embeddings"]
candidate_embeddings = y_pred["candidate_embeddings"]
labels = keras.ops.expand_dims(y, -1)
# Compute the affinity score by multiplying the two embeddings.
scores = keras.ops.sum(
keras.ops.multiply(query_embeddings, candidate_embeddings),
axis=1,
keepdims=True,
)
return self.loss_fn(labels, scores, sample_weight)
def compute_metrics(self, x, y, y_pred, sample_weight=None):
if "predictions" in y_pred:
# We are evaluating or predicting. Update `top_k_metric`.
movie_ids = x["movie_id"]
predictions = y_pred["predictions"]
# For `top_k_metric`, which is a `SparseTopKCategoricalAccuracy`, we
# only take top rated movies, and we put a weight of 0 for the rest.
rating_weight = keras.ops.cast(keras.ops.greater(y, 0.9), "float32")
sample_weight = (
rating_weight
if sample_weight is None
else keras.ops.multiply(rating_weight, sample_weight)
)
self.top_k_metric.update_state(
movie_ids, predictions, sample_weight=sample_weight
)
return self.get_metrics_result()
else:
# We are training. `top_k_metric` is not updated and is zero, so
# don't report it.
result = self.get_metrics_result()
result.pop(self.top_k_metric.name)
return result
训练模型
浅层模型
我们准备尝试我们的第一个浅层模型!
NUM_EPOCHS = 30
one_layer_model = RetrievalModel((32,))
one_layer_model.compile(optimizer=keras.optimizers.Adagrad(0.05))
one_layer_history = one_layer_model.fit(
train_ratings,
validation_data=test_ratings,
validation_freq=5,
epochs=NUM_EPOCHS,
)
Epoch 1/30
80/80 ━━━━━━━━━━━━━━━━━━━━ 19s 18ms/step - loss: 0.2392
Epoch 2/30
80/80 ━━━━━━━━━━━━━━━━━━━━ 1s 4ms/step - loss: 0.0764
Epoch 3/30
80/80 ━━━━━━━━━━━━━━━━━━━━ 0s 4ms/step - loss: 0.0748
Epoch 4/30
80/80 ━━━━━━━━━━━━━━━━━━━━ 0s 4ms/step - loss: 0.0737
Epoch 5/30
80/80 ━━━━━━━━━━━━━━━━━━━━ 19s 242ms/step - loss: 0.0727 - val_loss: 0.0736 - val_sparse_top_k_categorical_accuracy: 0.1196
Epoch 6/30
80/80 ━━━━━━━━━━━━━━━━━━━━ 0s 4ms/step - loss: 0.0718
Epoch 7/30
80/80 ━━━━━━━━━━━━━━━━━━━━ 0s 4ms/step - loss: 0.0710
Epoch 8/30
80/80 ━━━━━━━━━━━━━━━━━━━━ 0s 4ms/step - loss: 0.0702
Epoch 9/30
80/80 ━━━━━━━━━━━━━━━━━━━━ 0s 4ms/step - loss: 0.0694
Epoch 10/30
80/80 ━━━━━━━━━━━━━━━━━━━━ 0s 6ms/step - loss: 0.0685 - val_loss: 0.0695 - val_sparse_top_k_categorical_accuracy: 0.2117
Epoch 11/30
80/80 ━━━━━━━━━━━━━━━━━━━━ 0s 4ms/step - loss: 0.0677
Epoch 12/30
80/80 ━━━━━━━━━━━━━━━━━━━━ 0s 4ms/step - loss: 0.0669
Epoch 13/30
80/80 ━━━━━━━━━━━━━━━━━━━━ 0s 4ms/step - loss: 0.0661
Epoch 14/30
80/80 ━━━━━━━━━━━━━━━━━━━━ 0s 4ms/step - loss: 0.0653
Epoch 15/30
80/80 ━━━━━━━━━━━━━━━━━━━━ 0s 6ms/step - loss: 0.0645 - val_loss: 0.0655 - val_sparse_top_k_categorical_accuracy: 0.2742
Epoch 16/30
80/80 ━━━━━━━━━━━━━━━━━━━━ 0s 4ms/step - loss: 0.0637
Epoch 17/30
80/80 ━━━━━━━━━━━━━━━━━━━━ 0s 4ms/step - loss: 0.0629
Epoch 18/30
80/80 ━━━━━━━━━━━━━━━━━━━━ 0s 4ms/step - loss: 0.0622
Epoch 19/30
80/80 ━━━━━━━━━━━━━━━━━━━━ 0s 4ms/step - loss: 0.0615
Epoch 20/30
80/80 ━━━━━━━━━━━━━━━━━━━━ 0s 6ms/step - loss: 0.0608 - val_loss: 0.0621 - val_sparse_top_k_categorical_accuracy: 0.2994
Epoch 21/30
80/80 ━━━━━━━━━━━━━━━━━━━━ 0s 4ms/step - loss: 0.0602
Epoch 22/30
80/80 ━━━━━━━━━━━━━━━━━━━━ 0s 4ms/step - loss: 0.0596
Epoch 23/30
80/80 ━━━━━━━━━━━━━━━━━━━━ 0s 4ms/step - loss: 0.0590
Epoch 24/30
80/80 ━━━━━━━━━━━━━━━━━━━━ 0s 4ms/step - loss: 0.0585
Epoch 25/30
80/80 ━━━━━━━━━━━━━━━━━━━━ 0s 6ms/step - loss: 0.0580 - val_loss: 0.0596 - val_sparse_top_k_categorical_accuracy: 0.3150
Epoch 26/30
80/80 ━━━━━━━━━━━━━━━━━━━━ 0s 4ms/step - loss: 0.0576
Epoch 27/30
80/80 ━━━━━━━━━━━━━━━━━━━━ 0s 4ms/step - loss: 0.0572
Epoch 28/30
80/80 ━━━━━━━━━━━━━━━━━━━━ 0s 4ms/step - loss: 0.0569
Epoch 29/30
80/80 ━━━━━━━━━━━━━━━━━━━━ 0s 4ms/step - loss: 0.0565
Epoch 30/30
80/80 ━━━━━━━━━━━━━━━━━━━━ 1s 7ms/step - loss: 0.0562 - val_loss: 0.0581 - val_sparse_top_k_categorical_accuracy: 0.3100
这给了我们大约 0.30 的 Top-100 准确率。我们可以将其作为评估更深层模型的参考点。
更深层模型
那有两层的更深层模型呢?
two_layer_model = RetrievalModel((64, 32))
two_layer_model.compile(optimizer=keras.optimizers.Adagrad(0.05))
two_layer_history = two_layer_model.fit(
train_ratings,
validation_data=test_ratings,
validation_freq=5,
epochs=NUM_EPOCHS,
)
Epoch 1/30
80/80 ━━━━━━━━━━━━━━━━━━━━ 2s 15ms/step - loss: 0.2066
Epoch 2/30
80/80 ━━━━━━━━━━━━━━━━━━━━ 1s 4ms/step - loss: 0.0756
Epoch 3/30
80/80 ━━━━━━━━━━━━━━━━━━━━ 0s 4ms/step - loss: 0.0736
Epoch 4/30
80/80 ━━━━━━━━━━━━━━━━━━━━ 0s 4ms/step - loss: 0.0721
Epoch 5/30
80/80 ━━━━━━━━━━━━━━━━━━━━ 2s 25ms/step - loss: 0.0708 - val_loss: 0.0713 - val_sparse_top_k_categorical_accuracy: 0.1530
Epoch 6/30
80/80 ━━━━━━━━━━━━━━━━━━━━ 0s 4ms/step - loss: 0.0696
Epoch 7/30
80/80 ━━━━━━━━━━━━━━━━━━━━ 0s 4ms/step - loss: 0.0685
Epoch 8/30
80/80 ━━━━━━━━━━━━━━━━━━━━ 1s 8ms/step - loss: 0.0675
Epoch 9/30
80/80 ━━━━━━━━━━━━━━━━━━━━ 0s 4ms/step - loss: 0.0664
Epoch 10/30
80/80 ━━━━━━━━━━━━━━━━━━━━ 1s 6ms/step - loss: 0.0654 - val_loss: 0.0661 - val_sparse_top_k_categorical_accuracy: 0.2355
Epoch 11/30
80/80 ━━━━━━━━━━━━━━━━━━━━ 0s 4ms/step - loss: 0.0644
Epoch 12/30
80/80 ━━━━━━━━━━━━━━━━━━━━ 0s 4ms/step - loss: 0.0634
Epoch 13/30
80/80 ━━━━━━━━━━━━━━━━━━━━ 0s 4ms/step - loss: 0.0625
Epoch 14/30
80/80 ━━━━━━━━━━━━━━━━━━━━ 0s 4ms/step - loss: 0.0616
Epoch 15/30
80/80 ━━━━━━━━━━━━━━━━━━━━ 0s 6ms/step - loss: 0.0608 - val_loss: 0.0618 - val_sparse_top_k_categorical_accuracy: 0.2882
Epoch 16/30
80/80 ━━━━━━━━━━━━━━━━━━━━ 0s 4ms/step - loss: 0.0600
Epoch 17/30
80/80 ━━━━━━━━━━━━━━━━━━━━ 0s 4ms/step - loss: 0.0594
Epoch 18/30
80/80 ━━━━━━━━━━━━━━━━━━━━ 0s 4ms/step - loss: 0.0587
Epoch 19/30
80/80 ━━━━━━━━━━━━━━━━━━━━ 0s 4ms/step - loss: 0.0582
Epoch 20/30
80/80 ━━━━━━━━━━━━━━━━━━━━ 1s 10ms/step - loss: 0.0577 - val_loss: 0.0591 - val_sparse_top_k_categorical_accuracy: 0.3072
Epoch 21/30
80/80 ━━━━━━━━━━━━━━━━━━━━ 0s 4ms/step - loss: 0.0573
Epoch 22/30
80/80 ━━━━━━━━━━━━━━━━━━━━ 0s 4ms/step - loss: 0.0569
Epoch 23/30
80/80 ━━━━━━━━━━━━━━━━━━━━ 0s 4ms/step - loss: 0.0566
Epoch 24/30
80/80 ━━━━━━━━━━━━━━━━━━━━ 0s 4ms/step - loss: 0.0562
Epoch 25/30
80/80 ━━━━━━━━━━━━━━━━━━━━ 0s 6ms/step - loss: 0.0560 - val_loss: 0.0577 - val_sparse_top_k_categorical_accuracy: 0.3134
Epoch 26/30
80/80 ━━━━━━━━━━━━━━━━━━━━ 0s 4ms/step - loss: 0.0557
Epoch 27/30
80/80 ━━━━━━━━━━━━━━━━━━━━ 0s 4ms/step - loss: 0.0555
Epoch 28/30
80/80 ━━━━━━━━━━━━━━━━━━━━ 0s 4ms/step - loss: 0.0553
Epoch 29/30
80/80 ━━━━━━━━━━━━━━━━━━━━ 0s 4ms/step - loss: 0.0551
Epoch 30/30
80/80 ━━━━━━━━━━━━━━━━━━━━ 1s 6ms/step - loss: 0.0549 - val_loss: 0.0569 - val_sparse_top_k_categorical_accuracy: 0.3093
虽然更深的模型在开始时似乎比浅层模型学习得更好,但在训练结束时差异变得很小。我们可以绘制验证准确率曲线来说明这一点。
METRIC = "val_sparse_top_k_categorical_accuracy"
num_validation_runs = len(one_layer_history.history[METRIC])
epochs = [(x + 1) * 5 for x in range(num_validation_runs)]
plt.plot(epochs, one_layer_history.history[METRIC], label="1 layer")
plt.plot(epochs, two_layer_history.history[METRIC], label="2 layers")
plt.title("Accuracy vs epoch")
plt.xlabel("epoch")
plt.ylabel("Top-100 accuracy")
plt.legend()
plt.show()
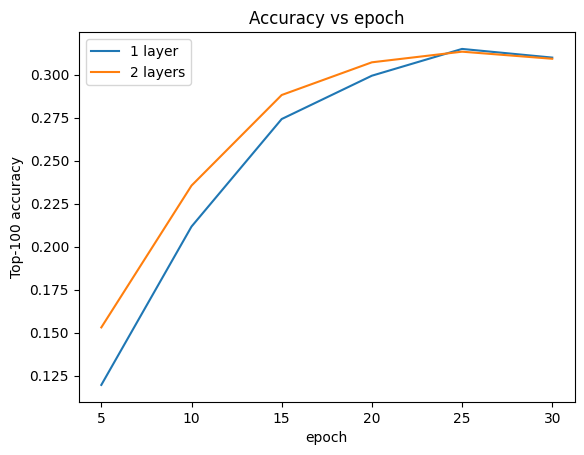
更深的模型不一定更好。以下模型将深度扩展到三层。
three_layer_model = RetrievalModel((128, 64, 32))
three_layer_model.compile(optimizer=keras.optimizers.Adagrad(0.05))
three_layer_history = three_layer_model.fit(
train_ratings,
validation_data=test_ratings,
validation_freq=5,
epochs=NUM_EPOCHS,
)
Epoch 1/30
80/80 ━━━━━━━━━━━━━━━━━━━━ 3s 17ms/step - loss: 0.1880
Epoch 2/30
80/80 ━━━━━━━━━━━━━━━━━━━━ 1s 4ms/step - loss: 0.0751
Epoch 3/30
80/80 ━━━━━━━━━━━━━━━━━━━━ 0s 4ms/step - loss: 0.0734
Epoch 4/30
80/80 ━━━━━━━━━━━━━━━━━━━━ 0s 4ms/step - loss: 0.0720
Epoch 5/30
80/80 ━━━━━━━━━━━━━━━━━━━━ 2s 26ms/step - loss: 0.0707 - val_loss: 0.0712 - val_sparse_top_k_categorical_accuracy: 0.1276
Epoch 6/30
80/80 ━━━━━━━━━━━━━━━━━━━━ 0s 4ms/step - loss: 0.0694
Epoch 7/30
80/80 ━━━━━━━━━━━━━━━━━━━━ 0s 5ms/step - loss: 0.0682
Epoch 8/30
80/80 ━━━━━━━━━━━━━━━━━━━━ 0s 4ms/step - loss: 0.0670
Epoch 9/30
80/80 ━━━━━━━━━━━━━━━━━━━━ 0s 4ms/step - loss: 0.0659
Epoch 10/30
80/80 ━━━━━━━━━━━━━━━━━━━━ 1s 6ms/step - loss: 0.0648 - val_loss: 0.0656 - val_sparse_top_k_categorical_accuracy: 0.2552
Epoch 11/30
80/80 ━━━━━━━━━━━━━━━━━━━━ 0s 5ms/step - loss: 0.0637
Epoch 12/30
80/80 ━━━━━━━━━━━━━━━━━━━━ 0s 4ms/step - loss: 0.0628
Epoch 13/30
80/80 ━━━━━━━━━━━━━━━━━━━━ 0s 4ms/step - loss: 0.0618
Epoch 14/30
80/80 ━━━━━━━━━━━━━━━━━━━━ 0s 4ms/step - loss: 0.0610
Epoch 15/30
80/80 ━━━━━━━━━━━━━━━━━━━━ 1s 6ms/step - loss: 0.0603 - val_loss: 0.0616 - val_sparse_top_k_categorical_accuracy: 0.2816
Epoch 16/30
80/80 ━━━━━━━━━━━━━━━━━━━━ 0s 4ms/step - loss: 0.0596
Epoch 17/30
80/80 ━━━━━━━━━━━━━━━━━━━━ 0s 4ms/step - loss: 0.0590
Epoch 18/30
80/80 ━━━━━━━━━━━━━━━━━━━━ 0s 4ms/step - loss: 0.0584
Epoch 19/30
80/80 ━━━━━━━━━━━━━━━━━━━━ 0s 4ms/step - loss: 0.0579
Epoch 20/30
80/80 ━━━━━━━━━━━━━━━━━━━━ 1s 7ms/step - loss: 0.0575 - val_loss: 0.0592 - val_sparse_top_k_categorical_accuracy: 0.2921
Epoch 21/30
80/80 ━━━━━━━━━━━━━━━━━━━━ 0s 4ms/step - loss: 0.0571
Epoch 22/30
80/80 ━━━━━━━━━━━━━━━━━━━━ 0s 4ms/step - loss: 0.0567
Epoch 23/30
80/80 ━━━━━━━━━━━━━━━━━━━━ 0s 4ms/step - loss: 0.0564
Epoch 24/30
80/80 ━━━━━━━━━━━━━━━━━━━━ 0s 4ms/step - loss: 0.0561
Epoch 25/30
80/80 ━━━━━━━━━━━━━━━━━━━━ 1s 6ms/step - loss: 0.0559 - val_loss: 0.0578 - val_sparse_top_k_categorical_accuracy: 0.2983
Epoch 26/30
80/80 ━━━━━━━━━━━━━━━━━━━━ 0s 4ms/step - loss: 0.0557
Epoch 27/30
80/80 ━━━━━━━━━━━━━━━━━━━━ 0s 5ms/step - loss: 0.0555
Epoch 28/30
80/80 ━━━━━━━━━━━━━━━━━━━━ 0s 4ms/step - loss: 0.0553
Epoch 29/30
80/80 ━━━━━━━━━━━━━━━━━━━━ 0s 4ms/step - loss: 0.0551
Epoch 30/30
80/80 ━━━━━━━━━━━━━━━━━━━━ 1s 6ms/step - loss: 0.0549 - val_loss: 0.0571 - val_sparse_top_k_categorical_accuracy: 0.3006
我们实际上没有看到比浅层模型有任何改进。
plt.plot(epochs, one_layer_history.history[METRIC], label="1 layer")
plt.plot(epochs, two_layer_history.history[METRIC], label="2 layers")
plt.plot(epochs, three_layer_history.history[METRIC], label="3 layers")
plt.title("Accuracy vs epoch")
plt.xlabel("epoch")
plt.ylabel("Top-100 accuracy")
plt.legend()
plt.show()
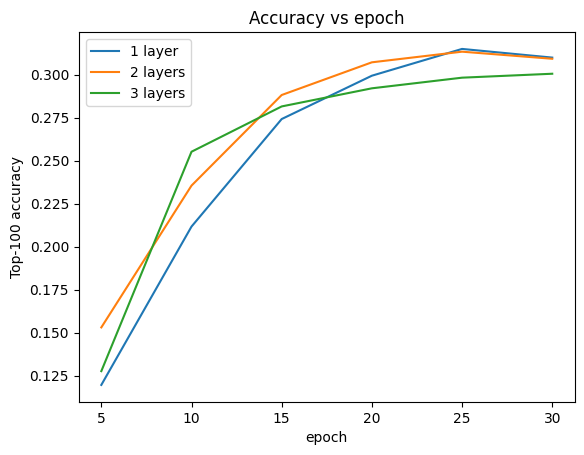
这很好地说明了更深、更大的模型虽然有潜力获得更好的性能,但通常需要非常细致的调优。例如,在本教程中,我们使用了一个单一的、固定的学习率。替代选择可能会产生非常不同的结果,值得探索。
通过适当的调优和足够的数据,在许多情况下,在构建更大、更深模型上付出的努力是值得的:更大的模型可以带来预测准确性的显著提高。
后续步骤
在本教程中,我们通过添加密集层和激活函数来扩展了我们的检索模型。要了解如何创建不仅可以执行检索任务,还可以执行评分任务的模型,请参阅多任务教程。