估算模型训练所需的样本量
作者: JacoVerster
创建日期 2021/05/20
最后修改日期 2021/06/06
描述: 模拟训练集大小与模型准确率之间的关系。
简介
在许多实际场景中,用于训练深度学习模型的图像数据量是有限的。在医学影像领域尤其如此,因为数据集的创建成本很高。当着手解决一个新问题时,通常会问到的第一个问题是:“我们需要多少张图片才能训练出一个足够好的机器学习模型?”
在大多数情况下,我们会有一个小样本集,并可以利用它来模拟训练数据大小与模型性能之间的关系。这样的模型可以用来估计达到所需模型性能所需的最佳图片数量。
Balki 等人的 Sample-Size Determination Methodologies 综述提供了几种样本量确定方法的示例。在本示例中,使用平衡的子采样方案来确定模型的最佳样本量。这通过选择一个包含 Y 张图片的随机子集并使用该子集训练模型来实现。然后,模型将在独立的测试集上进行评估。为了能够构建观察到的性能的均值和置信区间,这个过程对每个子集重复 N 次(带放回)。
设置
import os
os.environ["KERAS_BACKEND"] = "tensorflow"
import matplotlib.pyplot as plt
import numpy as np
import tensorflow as tf
import keras
from keras import layers
import tensorflow_datasets as tfds
# Define seed and fixed variables
seed = 42
keras.utils.set_random_seed(seed)
AUTO = tf.data.AUTOTUNE
加载 TensorFlow 数据集并转换为 NumPy 数组
我们将使用 TF Flowers 数据集。
# Specify dataset parameters
dataset_name = "tf_flowers"
batch_size = 64
image_size = (224, 224)
# Load data from tfds and split 10% off for a test set
(train_data, test_data), ds_info = tfds.load(
dataset_name,
split=["train[:90%]", "train[90%:]"],
shuffle_files=True,
as_supervised=True,
with_info=True,
)
# Extract number of classes and list of class names
num_classes = ds_info.features["label"].num_classes
class_names = ds_info.features["label"].names
print(f"Number of classes: {num_classes}")
print(f"Class names: {class_names}")
# Convert datasets to NumPy arrays
def dataset_to_array(dataset, image_size, num_classes):
images, labels = [], []
for img, lab in dataset.as_numpy_iterator():
images.append(tf.image.resize(img, image_size).numpy())
labels.append(tf.one_hot(lab, num_classes))
return np.array(images), np.array(labels)
img_train, label_train = dataset_to_array(train_data, image_size, num_classes)
img_test, label_test = dataset_to_array(test_data, image_size, num_classes)
num_train_samples = len(img_train)
print(f"Number of training samples: {num_train_samples}")
Number of classes: 5
Class names: ['dandelion', 'daisy', 'tulips', 'sunflowers', 'roses']
Number of training samples: 3303
绘制测试集中的一些示例
plt.figure(figsize=(16, 12))
for n in range(30):
ax = plt.subplot(5, 6, n + 1)
plt.imshow(img_test[n].astype("uint8"))
plt.title(np.array(class_names)[label_test[n] == True][0])
plt.axis("off")
数据增强
使用 Keras 预处理层定义图像增强,并将其应用于训练集。
# Define image augmentation model
image_augmentation = keras.Sequential(
[
layers.RandomFlip(mode="horizontal"),
layers.RandomRotation(factor=0.1),
layers.RandomZoom(height_factor=(-0.1, -0)),
layers.RandomContrast(factor=0.1),
],
)
# Apply the augmentations to the training images and plot a few examples
img_train = image_augmentation(img_train).numpy()
plt.figure(figsize=(16, 12))
for n in range(30):
ax = plt.subplot(5, 6, n + 1)
plt.imshow(img_train[n].astype("uint8"))
plt.title(np.array(class_names)[label_train[n] == True][0])
plt.axis("off")

定义模型构建和训练函数
我们创建了几个便捷函数来构建迁移学习模型、编译和训练模型,以及解冻层进行微调。
def build_model(num_classes, img_size=image_size[0], top_dropout=0.3):
"""Creates a classifier based on pre-trained MobileNetV2.
Arguments:
num_classes: Int, number of classese to use in the softmax layer.
img_size: Int, square size of input images (defaults is 224).
top_dropout: Int, value for dropout layer (defaults is 0.3).
Returns:
Uncompiled Keras model.
"""
# Create input and pre-processing layers for MobileNetV2
inputs = layers.Input(shape=(img_size, img_size, 3))
x = layers.Rescaling(scale=1.0 / 127.5, offset=-1)(inputs)
model = keras.applications.MobileNetV2(
include_top=False, weights="imagenet", input_tensor=x
)
# Freeze the pretrained weights
model.trainable = False
# Rebuild top
x = layers.GlobalAveragePooling2D(name="avg_pool")(model.output)
x = layers.Dropout(top_dropout)(x)
outputs = layers.Dense(num_classes, activation="softmax")(x)
model = keras.Model(inputs, outputs)
print("Trainable weights:", len(model.trainable_weights))
print("Non_trainable weights:", len(model.non_trainable_weights))
return model
def compile_and_train(
model,
training_data,
training_labels,
metrics=[keras.metrics.AUC(name="auc"), "acc"],
optimizer=keras.optimizers.Adam(),
patience=5,
epochs=5,
):
"""Compiles and trains the model.
Arguments:
model: Uncompiled Keras model.
training_data: NumPy Array, training data.
training_labels: NumPy Array, training labels.
metrics: Keras/TF metrics, requires at least 'auc' metric (default is
`[keras.metrics.AUC(name='auc'), 'acc']`).
optimizer: Keras/TF optimizer (defaults is `keras.optimizers.Adam()).
patience: Int, epochsfor EarlyStopping patience (defaults is 5).
epochs: Int, number of epochs to train (default is 5).
Returns:
Training history for trained Keras model.
"""
stopper = keras.callbacks.EarlyStopping(
monitor="val_auc",
mode="max",
min_delta=0,
patience=patience,
verbose=1,
restore_best_weights=True,
)
model.compile(loss="categorical_crossentropy", optimizer=optimizer, metrics=metrics)
history = model.fit(
x=training_data,
y=training_labels,
batch_size=batch_size,
epochs=epochs,
validation_split=0.1,
callbacks=[stopper],
)
return history
def unfreeze(model, block_name, verbose=0):
"""Unfreezes Keras model layers.
Arguments:
model: Keras model.
block_name: Str, layer name for example block_name = 'block4'.
Checks if supplied string is in the layer name.
verbose: Int, 0 means silent, 1 prints out layers trainability status.
Returns:
Keras model with all layers after (and including) the specified
block_name to trainable, excluding BatchNormalization layers.
"""
# Unfreeze from block_name onwards
set_trainable = False
for layer in model.layers:
if block_name in layer.name:
set_trainable = True
if set_trainable and not isinstance(layer, layers.BatchNormalization):
layer.trainable = True
if verbose == 1:
print(layer.name, "trainable")
else:
if verbose == 1:
print(layer.name, "NOT trainable")
print("Trainable weights:", len(model.trainable_weights))
print("Non-trainable weights:", len(model.non_trainable_weights))
return model
定义迭代训练函数
为了在多个子集上训练模型,我们需要创建一个迭代训练函数。
def train_model(training_data, training_labels):
"""Trains the model as follows:
- Trains only the top layers for 10 epochs.
- Unfreezes deeper layers.
- Train for 20 more epochs.
Arguments:
training_data: NumPy Array, training data.
training_labels: NumPy Array, training labels.
Returns:
Model accuracy.
"""
model = build_model(num_classes)
# Compile and train top layers
history = compile_and_train(
model,
training_data,
training_labels,
metrics=[keras.metrics.AUC(name="auc"), "acc"],
optimizer=keras.optimizers.Adam(),
patience=3,
epochs=10,
)
# Unfreeze model from block 10 onwards
model = unfreeze(model, "block_10")
# Compile and train for 20 epochs with a lower learning rate
fine_tune_epochs = 20
total_epochs = history.epoch[-1] + fine_tune_epochs
history_fine = compile_and_train(
model,
training_data,
training_labels,
metrics=[keras.metrics.AUC(name="auc"), "acc"],
optimizer=keras.optimizers.Adam(learning_rate=1e-4),
patience=5,
epochs=total_epochs,
)
# Calculate model accuracy on the test set
_, _, acc = model.evaluate(img_test, label_test)
return np.round(acc, 4)
迭代训练模型
既然我们有了模型构建函数和支持的迭代函数,我们就可以在多个子集划分上训练模型了。
- 我们选择子集划分为下载数据集的 5%、10%、25% 和 50%。我们假设目前只有实际数据的 50% 可用。
- 我们在每个划分上从头开始训练模型 5 次,并记录准确率值。
请注意,这将训练 20 个模型,需要一些时间。请确保您已激活 GPU 运行时。
为了使本示例保持轻量级,我们提供了之前训练运行的样本数据。
def train_iteratively(sample_splits=[0.05, 0.1, 0.25, 0.5], iter_per_split=5):
"""Trains a model iteratively over several sample splits.
Arguments:
sample_splits: List/NumPy array, contains fractions of the trainins set
to train over.
iter_per_split: Int, number of times to train a model per sample split.
Returns:
Training accuracy for all splits and iterations and the number of samples
used for training at each split.
"""
# Train all the sample models and calculate accuracy
train_acc = []
sample_sizes = []
for fraction in sample_splits:
print(f"Fraction split: {fraction}")
# Repeat training 3 times for each sample size
sample_accuracy = []
num_samples = int(num_train_samples * fraction)
for i in range(iter_per_split):
print(f"Run {i+1} out of {iter_per_split}:")
# Create fractional subsets
rand_idx = np.random.randint(num_train_samples, size=num_samples)
train_img_subset = img_train[rand_idx, :]
train_label_subset = label_train[rand_idx, :]
# Train model and calculate accuracy
accuracy = train_model(train_img_subset, train_label_subset)
print(f"Accuracy: {accuracy}")
sample_accuracy.append(accuracy)
train_acc.append(sample_accuracy)
sample_sizes.append(num_samples)
return train_acc, sample_sizes
# Running the above function produces the following outputs
train_acc = [
[0.8202, 0.7466, 0.8011, 0.8447, 0.8229],
[0.861, 0.8774, 0.8501, 0.8937, 0.891],
[0.891, 0.9237, 0.8856, 0.9101, 0.891],
[0.8937, 0.9373, 0.9128, 0.8719, 0.9128],
]
sample_sizes = [165, 330, 825, 1651]
学习曲线
我们现在通过将指数曲线拟合到平均准确率点来绘制学习曲线。我们使用 TF 将指数函数拟合到数据上。
然后,我们外推学习曲线,以预测在整个训练集上训练的模型的准确率。
def fit_and_predict(train_acc, sample_sizes, pred_sample_size):
"""Fits a learning curve to model training accuracy results.
Arguments:
train_acc: List/Numpy Array, training accuracy for all model
training splits and iterations.
sample_sizes: List/Numpy array, number of samples used for training at
each split.
pred_sample_size: Int, sample size to predict model accuracy based on
fitted learning curve.
"""
x = sample_sizes
mean_acc = tf.convert_to_tensor([np.mean(i) for i in train_acc])
error = [np.std(i) for i in train_acc]
# Define mean squared error cost and exponential curve fit functions
mse = keras.losses.MeanSquaredError()
def exp_func(x, a, b):
return a * x**b
# Define variables, learning rate and number of epochs for fitting with TF
a = tf.Variable(0.0)
b = tf.Variable(0.0)
learning_rate = 0.01
training_epochs = 5000
# Fit the exponential function to the data
for epoch in range(training_epochs):
with tf.GradientTape() as tape:
y_pred = exp_func(x, a, b)
cost_function = mse(y_pred, mean_acc)
# Get gradients and compute adjusted weights
gradients = tape.gradient(cost_function, [a, b])
a.assign_sub(gradients[0] * learning_rate)
b.assign_sub(gradients[1] * learning_rate)
print(f"Curve fit weights: a = {a.numpy()} and b = {b.numpy()}.")
# We can now estimate the accuracy for pred_sample_size
max_acc = exp_func(pred_sample_size, a, b).numpy()
# Print predicted x value and append to plot values
print(f"A model accuracy of {max_acc} is predicted for {pred_sample_size} samples.")
x_cont = np.linspace(x[0], pred_sample_size, 100)
# Build the plot
fig, ax = plt.subplots(figsize=(12, 6))
ax.errorbar(x, mean_acc, yerr=error, fmt="o", label="Mean acc & std dev.")
ax.plot(x_cont, exp_func(x_cont, a, b), "r-", label="Fitted exponential curve.")
ax.set_ylabel("Model classification accuracy.", fontsize=12)
ax.set_xlabel("Training sample size.", fontsize=12)
ax.set_xticks(np.append(x, pred_sample_size))
ax.set_yticks(np.append(mean_acc, max_acc))
ax.set_xticklabels(list(np.append(x, pred_sample_size)), rotation=90, fontsize=10)
ax.yaxis.set_tick_params(labelsize=10)
ax.set_title("Learning curve: model accuracy vs sample size.", fontsize=14)
ax.legend(loc=(0.75, 0.75), fontsize=10)
ax.xaxis.grid(True)
ax.yaxis.grid(True)
plt.tight_layout()
plt.show()
# The mean absolute error (MAE) is calculated for curve fit to see how well
# it fits the data. The lower the error the better the fit.
mae = keras.losses.MeanAbsoluteError()
print(f"The mae for the curve fit is {mae(mean_acc, exp_func(x, a, b)).numpy()}.")
# We use the whole training set to predict the model accuracy
fit_and_predict(train_acc, sample_sizes, pred_sample_size=num_train_samples)
Curve fit weights: a = 0.6445642113685608 and b = 0.048097413033246994.
A model accuracy of 0.9517362117767334 is predicted for 3303 samples.
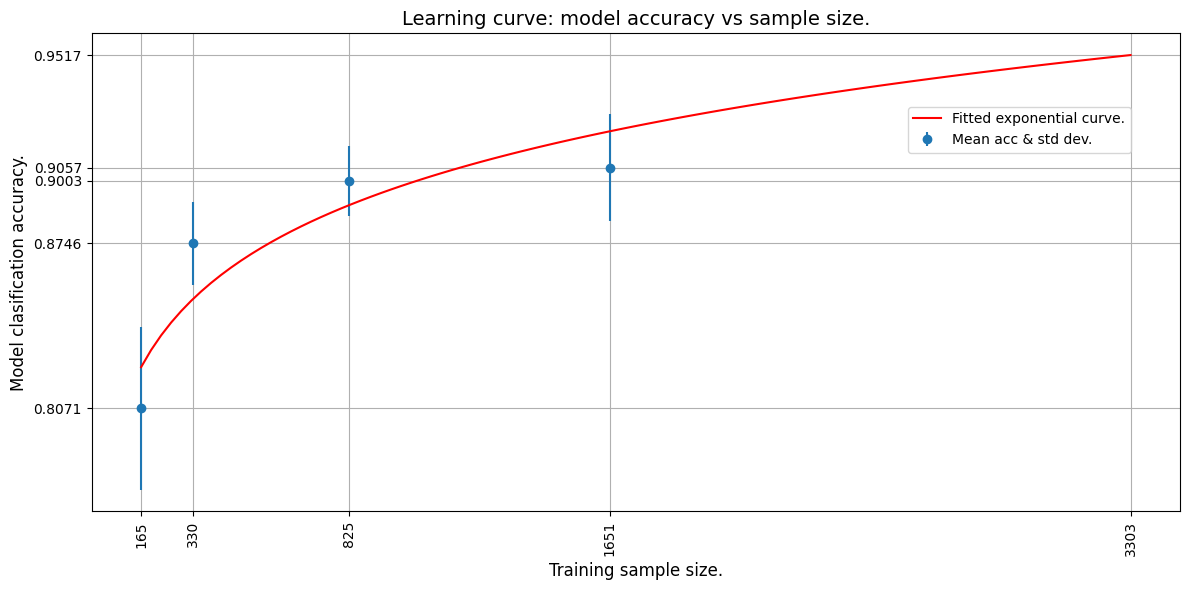
The mae for the curve fit is 0.016098767518997192.
从外推曲线可以看出,3303 张图片将产生约 95% 的估计准确率。
现在,让我们使用所有数据(3303 张图片)并训练模型,看看我们的预测是否准确!
# Now train the model with full dataset to get the actual accuracy
accuracy = train_model(img_train, label_train)
print(f"A model accuracy of {accuracy} is reached on {num_train_samples} images!")
/var/folders/8n/8w8cqnvj01xd4ghznl11nyn000_93_/T/ipykernel_30919/1838736464.py:16: UserWarning: `input_shape` is undefined or non-square, or `rows` is not in [96, 128, 160, 192, 224]. Weights for input shape (224, 224) will be loaded as the default.
model = keras.applications.MobileNetV2(
Trainable weights: 2
Non_trainable weights: 260
Epoch 1/10
47/47 ━━━━━━━━━━━━━━━━━━━━ 18s 338ms/step - acc: 0.4305 - auc: 0.7221 - loss: 1.4585 - val_acc: 0.8218 - val_auc: 0.9700 - val_loss: 0.5043
Epoch 2/10
47/47 ━━━━━━━━━━━━━━━━━━━━ 15s 326ms/step - acc: 0.7666 - auc: 0.9504 - loss: 0.6287 - val_acc: 0.8792 - val_auc: 0.9838 - val_loss: 0.3733
Epoch 3/10
47/47 ━━━━━━━━━━━━━━━━━━━━ 16s 332ms/step - acc: 0.8252 - auc: 0.9673 - loss: 0.5039 - val_acc: 0.8852 - val_auc: 0.9880 - val_loss: 0.3182
Epoch 4/10
47/47 ━━━━━━━━━━━━━━━━━━━━ 16s 348ms/step - acc: 0.8458 - auc: 0.9768 - loss: 0.4264 - val_acc: 0.8822 - val_auc: 0.9893 - val_loss: 0.2956
Epoch 5/10
47/47 ━━━━━━━━━━━━━━━━━━━━ 16s 350ms/step - acc: 0.8661 - auc: 0.9812 - loss: 0.3821 - val_acc: 0.8912 - val_auc: 0.9903 - val_loss: 0.2755
Epoch 6/10
47/47 ━━━━━━━━━━━━━━━━━━━━ 16s 336ms/step - acc: 0.8656 - auc: 0.9836 - loss: 0.3555 - val_acc: 0.9003 - val_auc: 0.9906 - val_loss: 0.2701
Epoch 7/10
47/47 ━━━━━━━━━━━━━━━━━━━━ 16s 331ms/step - acc: 0.8800 - auc: 0.9846 - loss: 0.3430 - val_acc: 0.8943 - val_auc: 0.9914 - val_loss: 0.2548
Epoch 8/10
47/47 ━━━━━━━━━━━━━━━━━━━━ 16s 333ms/step - acc: 0.8917 - auc: 0.9871 - loss: 0.3143 - val_acc: 0.8973 - val_auc: 0.9917 - val_loss: 0.2494
Epoch 9/10
47/47 ━━━━━━━━━━━━━━━━━━━━ 15s 320ms/step - acc: 0.9003 - auc: 0.9891 - loss: 0.2906 - val_acc: 0.9063 - val_auc: 0.9908 - val_loss: 0.2463
Epoch 10/10
47/47 ━━━━━━━━━━━━━━━━━━━━ 15s 324ms/step - acc: 0.8997 - auc: 0.9895 - loss: 0.2839 - val_acc: 0.9124 - val_auc: 0.9912 - val_loss: 0.2394
Trainable weights: 24
Non-trainable weights: 238
Epoch 1/29
47/47 ━━━━━━━━━━━━━━━━━━━━ 27s 537ms/step - acc: 0.8457 - auc: 0.9747 - loss: 0.4365 - val_acc: 0.9094 - val_auc: 0.9916 - val_loss: 0.2692
Epoch 2/29
47/47 ━━━━━━━━━━━━━━━━━━━━ 24s 502ms/step - acc: 0.9223 - auc: 0.9932 - loss: 0.2198 - val_acc: 0.9033 - val_auc: 0.9891 - val_loss: 0.2826
Epoch 3/29
47/47 ━━━━━━━━━━━━━━━━━━━━ 25s 534ms/step - acc: 0.9499 - auc: 0.9972 - loss: 0.1399 - val_acc: 0.9003 - val_auc: 0.9910 - val_loss: 0.2804
Epoch 4/29
47/47 ━━━━━━━━━━━━━━━━━━━━ 26s 554ms/step - acc: 0.9590 - auc: 0.9983 - loss: 0.1130 - val_acc: 0.9396 - val_auc: 0.9968 - val_loss: 0.1510
Epoch 5/29
47/47 ━━━━━━━━━━━━━━━━━━━━ 25s 533ms/step - acc: 0.9805 - auc: 0.9996 - loss: 0.0538 - val_acc: 0.9486 - val_auc: 0.9914 - val_loss: 0.1795
Epoch 6/29
47/47 ━━━━━━━━━━━━━━━━━━━━ 24s 516ms/step - acc: 0.9949 - auc: 1.0000 - loss: 0.0226 - val_acc: 0.9124 - val_auc: 0.9833 - val_loss: 0.3186
Epoch 7/29
47/47 ━━━━━━━━━━━━━━━━━━━━ 25s 534ms/step - acc: 0.9900 - auc: 0.9999 - loss: 0.0297 - val_acc: 0.9275 - val_auc: 0.9881 - val_loss: 0.3017
Epoch 8/29
47/47 ━━━━━━━━━━━━━━━━━━━━ 25s 536ms/step - acc: 0.9910 - auc: 0.9999 - loss: 0.0228 - val_acc: 0.9426 - val_auc: 0.9927 - val_loss: 0.1938
Epoch 9/29
47/47 ━━━━━━━━━━━━━━━━━━━━ 0s 489ms/step - acc: 0.9995 - auc: 1.0000 - loss: 0.0069Restoring model weights from the end of the best epoch: 4.
47/47 ━━━━━━━━━━━━━━━━━━━━ 25s 527ms/step - acc: 0.9995 - auc: 1.0000 - loss: 0.0068 - val_acc: 0.9426 - val_auc: 0.9919 - val_loss: 0.2957
Epoch 9: early stopping
12/12 ━━━━━━━━━━━━━━━━━━━━ 2s 170ms/step - acc: 0.9641 - auc: 0.9972 - loss: 0.1264
A model accuracy of 0.9964 is reached on 3303 images!
结论
我们看到,使用 3303 张图片达到了大约 94-96%* 的模型准确率。这与我们的估计非常接近!
尽管我们只使用了 50% 的数据集(1651 张图片),但我们能够模拟模型的训练行为,并预测给定图片数量下的模型准确率。此方法可用于预测达到所需准确率所需的图片数量。当可用的数据量较少,并且已有证据表明可以收敛到深度学习模型但需要更多图片时,这将非常有用。图片数量预测可用于规划和预算进一步的图片收集计划。