向量量化变分自编码器
作者:Sayak Paul
创建日期 2021/07/21
最后修改日期 2021/06/27
描述:训练一个 VQ-VAE 进行图像重建和码本采样以生成新图像。
在此示例中,我们开发一个向量量化变分自编码器 (VQ-VAE)。VQ-VAE 由 van der Oord 等人在 Neural Discrete Representation Learning 中提出。在标准的 VAE 中,潜在空间是连续的,并从高斯分布中采样。通常很难通过梯度下降来学习这种连续分布。而 VQ-VAE 在离散的潜在空间上操作,使得优化问题更简单。它通过维护一个离散的码本来实现这一点。码本是通过离散化连续嵌入与编码输出之间的距离来开发的。然后将这些离散码词馈送给解码器,解码器被训练来生成重建样本。
有关 VQ-VAE 的概述,请参阅原始论文和此视频解释。如果您需要复习 VAE,可以参考这本书的章节。VQ-VAE 是 DALL-E 背后的主要方法之一,码本的概念也用于 VQ-GAN。
此示例使用了 DeepMind 的官方 VQ-VAE 教程中的实现细节。
要求
要运行此示例,您需要 TensorFlow 2.5 或更高版本,以及 TensorFlow Probability,可以使用以下命令进行安装。
!pip install -q tensorflow-probability
导入
import numpy as np
import matplotlib.pyplot as plt
from tensorflow import keras
from tensorflow.keras import layers
import tensorflow_probability as tfp
import tensorflow as tf
VectorQuantizer 层
首先,我们为向量量化器实现一个自定义层,这是编码器和解码器之间的层。考虑来自编码器的输出,其形状为 (batch_size, height, width, num_filters)。向量量化器将首先展平此输出,仅保持 num_filters 维度不变。因此,形状将变为 (batch_size * height * width, num_filters)。这样做的理由是将滤波器总数视为潜在嵌入的大小。
然后初始化一个嵌入表来学习码本。我们测量展平的编码器输出与此码本的码词之间的 L2 归一化距离。我们取产生最小距离的码,并应用独热编码来实现量化。这样,与相应编码器输出距离最小的码被映射为 1,其余码被映射为 0。
由于量化过程不可微分,我们在解码器和编码器之间应用了一个直通估计器,以便解码器的梯度直接传播到编码器。由于编码器和解码器共享相同的通道空间,因此解码器梯度对编码器仍然有意义。
class VectorQuantizer(layers.Layer):
def __init__(self, num_embeddings, embedding_dim, beta=0.25, **kwargs):
super().__init__(**kwargs)
self.embedding_dim = embedding_dim
self.num_embeddings = num_embeddings
# The `beta` parameter is best kept between [0.25, 2] as per the paper.
self.beta = beta
# Initialize the embeddings which we will quantize.
w_init = tf.random_uniform_initializer()
self.embeddings = tf.Variable(
initial_value=w_init(
shape=(self.embedding_dim, self.num_embeddings), dtype="float32"
),
trainable=True,
name="embeddings_vqvae",
)
def call(self, x):
# Calculate the input shape of the inputs and
# then flatten the inputs keeping `embedding_dim` intact.
input_shape = tf.shape(x)
flattened = tf.reshape(x, [-1, self.embedding_dim])
# Quantization.
encoding_indices = self.get_code_indices(flattened)
encodings = tf.one_hot(encoding_indices, self.num_embeddings)
quantized = tf.matmul(encodings, self.embeddings, transpose_b=True)
# Reshape the quantized values back to the original input shape
quantized = tf.reshape(quantized, input_shape)
# Calculate vector quantization loss and add that to the layer. You can learn more
# about adding losses to different layers here:
# https://keras.org.cn/guides/making_new_layers_and_models_via_subclassing/. Check
# the original paper to get a handle on the formulation of the loss function.
commitment_loss = tf.reduce_mean((tf.stop_gradient(quantized) - x) ** 2)
codebook_loss = tf.reduce_mean((quantized - tf.stop_gradient(x)) ** 2)
self.add_loss(self.beta * commitment_loss + codebook_loss)
# Straight-through estimator.
quantized = x + tf.stop_gradient(quantized - x)
return quantized
def get_code_indices(self, flattened_inputs):
# Calculate L2-normalized distance between the inputs and the codes.
similarity = tf.matmul(flattened_inputs, self.embeddings)
distances = (
tf.reduce_sum(flattened_inputs ** 2, axis=1, keepdims=True)
+ tf.reduce_sum(self.embeddings ** 2, axis=0)
- 2 * similarity
)
# Derive the indices for minimum distances.
encoding_indices = tf.argmin(distances, axis=1)
return encoding_indices
关于直通估计的说明:
这行代码完成了直通估计部分:quantized = x + tf.stop_gradient(quantized - x)。在反向传播期间,(quantized - x) 不会被包含在计算图中,并且为 quantized 获得的梯度将被复制给 inputs。感谢这个视频帮助我理解这项技术。
编码器和解码器
现在是 VQ-VAE 的编码器和解码器。我们将它们保持得较小,以便它们的容量能够很好地适应 MNIST 数据集。编码器和解码器的实现来自这个示例。
请注意,除了 ReLU 之外的激活函数在量化架构的编码器和解码器层中可能不起作用:例如,Leaky ReLU 激活的层已被证明难以训练,导致模型难以恢复的间歇性损失尖峰。
def get_encoder(latent_dim=16):
encoder_inputs = keras.Input(shape=(28, 28, 1))
x = layers.Conv2D(32, 3, activation="relu", strides=2, padding="same")(
encoder_inputs
)
x = layers.Conv2D(64, 3, activation="relu", strides=2, padding="same")(x)
encoder_outputs = layers.Conv2D(latent_dim, 1, padding="same")(x)
return keras.Model(encoder_inputs, encoder_outputs, name="encoder")
def get_decoder(latent_dim=16):
latent_inputs = keras.Input(shape=get_encoder(latent_dim).output.shape[1:])
x = layers.Conv2DTranspose(64, 3, activation="relu", strides=2, padding="same")(
latent_inputs
)
x = layers.Conv2DTranspose(32, 3, activation="relu", strides=2, padding="same")(x)
decoder_outputs = layers.Conv2DTranspose(1, 3, padding="same")(x)
return keras.Model(latent_inputs, decoder_outputs, name="decoder")
独立的 VQ-VAE 模型
def get_vqvae(latent_dim=16, num_embeddings=64):
vq_layer = VectorQuantizer(num_embeddings, latent_dim, name="vector_quantizer")
encoder = get_encoder(latent_dim)
decoder = get_decoder(latent_dim)
inputs = keras.Input(shape=(28, 28, 1))
encoder_outputs = encoder(inputs)
quantized_latents = vq_layer(encoder_outputs)
reconstructions = decoder(quantized_latents)
return keras.Model(inputs, reconstructions, name="vq_vae")
get_vqvae().summary()
Model: "vq_vae"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
input_4 (InputLayer) [(None, 28, 28, 1)] 0
_________________________________________________________________
encoder (Functional) (None, 7, 7, 16) 19856
_________________________________________________________________
vector_quantizer (VectorQuan (None, 7, 7, 16) 1024
_________________________________________________________________
decoder (Functional) (None, 28, 28, 1) 28033
=================================================================
Total params: 48,913
Trainable params: 48,913
Non-trainable params: 0
_________________________________________________________________
请注意,编码器的输出通道应与向量量化器的 latent_dim 匹配。
将训练循环包装在 VQVAETrainer 中
class VQVAETrainer(keras.models.Model):
def __init__(self, train_variance, latent_dim=32, num_embeddings=128, **kwargs):
super().__init__(**kwargs)
self.train_variance = train_variance
self.latent_dim = latent_dim
self.num_embeddings = num_embeddings
self.vqvae = get_vqvae(self.latent_dim, self.num_embeddings)
self.total_loss_tracker = keras.metrics.Mean(name="total_loss")
self.reconstruction_loss_tracker = keras.metrics.Mean(
name="reconstruction_loss"
)
self.vq_loss_tracker = keras.metrics.Mean(name="vq_loss")
@property
def metrics(self):
return [
self.total_loss_tracker,
self.reconstruction_loss_tracker,
self.vq_loss_tracker,
]
def train_step(self, x):
with tf.GradientTape() as tape:
# Outputs from the VQ-VAE.
reconstructions = self.vqvae(x)
# Calculate the losses.
reconstruction_loss = (
tf.reduce_mean((x - reconstructions) ** 2) / self.train_variance
)
total_loss = reconstruction_loss + sum(self.vqvae.losses)
# Backpropagation.
grads = tape.gradient(total_loss, self.vqvae.trainable_variables)
self.optimizer.apply_gradients(zip(grads, self.vqvae.trainable_variables))
# Loss tracking.
self.total_loss_tracker.update_state(total_loss)
self.reconstruction_loss_tracker.update_state(reconstruction_loss)
self.vq_loss_tracker.update_state(sum(self.vqvae.losses))
# Log results.
return {
"loss": self.total_loss_tracker.result(),
"reconstruction_loss": self.reconstruction_loss_tracker.result(),
"vqvae_loss": self.vq_loss_tracker.result(),
}
加载和预处理 MNIST 数据集
(x_train, _), (x_test, _) = keras.datasets.mnist.load_data()
x_train = np.expand_dims(x_train, -1)
x_test = np.expand_dims(x_test, -1)
x_train_scaled = (x_train / 255.0) - 0.5
x_test_scaled = (x_test / 255.0) - 0.5
data_variance = np.var(x_train / 255.0)
Downloading data from https://storage.googleapis.com/tensorflow/tf-keras-datasets/mnist.npz
11493376/11490434 [==============================] - 0s 0us/step
训练 VQ-VAE 模型
vqvae_trainer = VQVAETrainer(data_variance, latent_dim=16, num_embeddings=128)
vqvae_trainer.compile(optimizer=keras.optimizers.Adam())
vqvae_trainer.fit(x_train_scaled, epochs=30, batch_size=128)
Epoch 1/30
469/469 [==============================] - 18s 6ms/step - loss: 2.2962 - reconstruction_loss: 0.3869 - vqvae_loss: 1.5950
Epoch 2/30
469/469 [==============================] - 3s 6ms/step - loss: 2.2980 - reconstruction_loss: 0.1692 - vqvae_loss: 2.1108
Epoch 3/30
469/469 [==============================] - 3s 6ms/step - loss: 1.1356 - reconstruction_loss: 0.1281 - vqvae_loss: 0.9997
Epoch 4/30
469/469 [==============================] - 3s 6ms/step - loss: 0.6112 - reconstruction_loss: 0.1030 - vqvae_loss: 0.5031
Epoch 5/30
469/469 [==============================] - 3s 6ms/step - loss: 0.4375 - reconstruction_loss: 0.0883 - vqvae_loss: 0.3464
Epoch 6/30
469/469 [==============================] - 3s 6ms/step - loss: 0.3579 - reconstruction_loss: 0.0788 - vqvae_loss: 0.2775
Epoch 7/30
469/469 [==============================] - 3s 5ms/step - loss: 0.3197 - reconstruction_loss: 0.0725 - vqvae_loss: 0.2457
Epoch 8/30
469/469 [==============================] - 3s 5ms/step - loss: 0.2960 - reconstruction_loss: 0.0673 - vqvae_loss: 0.2277
Epoch 9/30
469/469 [==============================] - 3s 5ms/step - loss: 0.2798 - reconstruction_loss: 0.0640 - vqvae_loss: 0.2152
Epoch 10/30
469/469 [==============================] - 3s 5ms/step - loss: 0.2681 - reconstruction_loss: 0.0612 - vqvae_loss: 0.2061
Epoch 11/30
469/469 [==============================] - 3s 6ms/step - loss: 0.2578 - reconstruction_loss: 0.0590 - vqvae_loss: 0.1986
Epoch 12/30
469/469 [==============================] - 3s 6ms/step - loss: 0.2551 - reconstruction_loss: 0.0574 - vqvae_loss: 0.1974
Epoch 13/30
469/469 [==============================] - 3s 6ms/step - loss: 0.2526 - reconstruction_loss: 0.0560 - vqvae_loss: 0.1961
Epoch 14/30
469/469 [==============================] - 3s 6ms/step - loss: 0.2485 - reconstruction_loss: 0.0546 - vqvae_loss: 0.1936
Epoch 15/30
469/469 [==============================] - 3s 6ms/step - loss: 0.2462 - reconstruction_loss: 0.0533 - vqvae_loss: 0.1926
Epoch 16/30
469/469 [==============================] - 3s 6ms/step - loss: 0.2445 - reconstruction_loss: 0.0523 - vqvae_loss: 0.1920
Epoch 17/30
469/469 [==============================] - 3s 6ms/step - loss: 0.2427 - reconstruction_loss: 0.0515 - vqvae_loss: 0.1911
Epoch 18/30
469/469 [==============================] - 3s 6ms/step - loss: 0.2405 - reconstruction_loss: 0.0505 - vqvae_loss: 0.1898
Epoch 19/30
469/469 [==============================] - 3s 6ms/step - loss: 0.2368 - reconstruction_loss: 0.0495 - vqvae_loss: 0.1871
Epoch 20/30
469/469 [==============================] - 3s 5ms/step - loss: 0.2310 - reconstruction_loss: 0.0486 - vqvae_loss: 0.1822
Epoch 21/30
469/469 [==============================] - 3s 5ms/step - loss: 0.2245 - reconstruction_loss: 0.0475 - vqvae_loss: 0.1769
Epoch 22/30
469/469 [==============================] - 3s 5ms/step - loss: 0.2205 - reconstruction_loss: 0.0469 - vqvae_loss: 0.1736
Epoch 23/30
469/469 [==============================] - 3s 5ms/step - loss: 0.2195 - reconstruction_loss: 0.0465 - vqvae_loss: 0.1730
Epoch 24/30
469/469 [==============================] - 3s 5ms/step - loss: 0.2187 - reconstruction_loss: 0.0461 - vqvae_loss: 0.1726
Epoch 25/30
469/469 [==============================] - 3s 5ms/step - loss: 0.2180 - reconstruction_loss: 0.0458 - vqvae_loss: 0.1721
Epoch 26/30
469/469 [==============================] - 3s 5ms/step - loss: 0.2163 - reconstruction_loss: 0.0454 - vqvae_loss: 0.1709
Epoch 27/30
469/469 [==============================] - 3s 5ms/step - loss: 0.2156 - reconstruction_loss: 0.0452 - vqvae_loss: 0.1704
Epoch 28/30
469/469 [==============================] - 3s 5ms/step - loss: 0.2146 - reconstruction_loss: 0.0449 - vqvae_loss: 0.1696
Epoch 29/30
469/469 [==============================] - 3s 5ms/step - loss: 0.2139 - reconstruction_loss: 0.0447 - vqvae_loss: 0.1692
Epoch 30/30
469/469 [==============================] - 3s 5ms/step - loss: 0.2127 - reconstruction_loss: 0.0444 - vqvae_loss: 0.1682
<tensorflow.python.keras.callbacks.History at 0x7f96402f4e50>
测试集上的重建结果
def show_subplot(original, reconstructed):
plt.subplot(1, 2, 1)
plt.imshow(original.squeeze() + 0.5)
plt.title("Original")
plt.axis("off")
plt.subplot(1, 2, 2)
plt.imshow(reconstructed.squeeze() + 0.5)
plt.title("Reconstructed")
plt.axis("off")
plt.show()
trained_vqvae_model = vqvae_trainer.vqvae
idx = np.random.choice(len(x_test_scaled), 10)
test_images = x_test_scaled[idx]
reconstructions_test = trained_vqvae_model.predict(test_images)
for test_image, reconstructed_image in zip(test_images, reconstructions_test):
show_subplot(test_image, reconstructed_image)
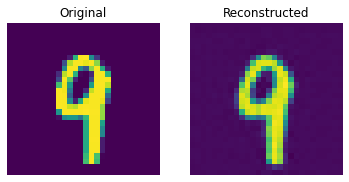
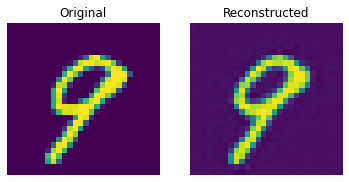

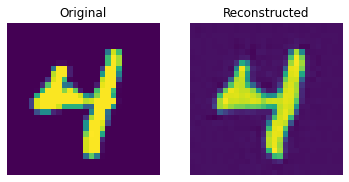
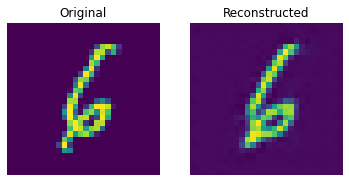
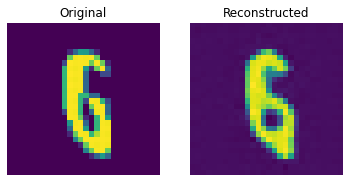
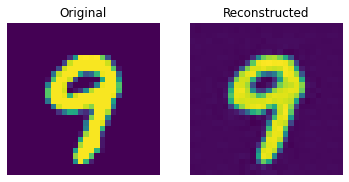
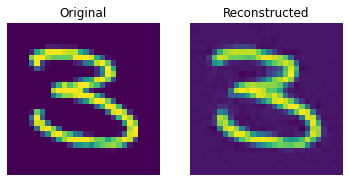
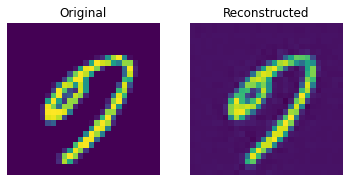
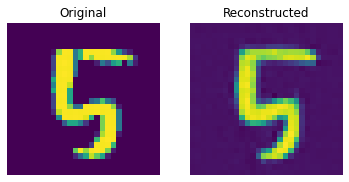
这些结果看起来不错。我们鼓励您尝试不同的超参数(尤其是嵌入的数量和嵌入的维度),并观察它们如何影响结果。
可视化离散码
encoder = vqvae_trainer.vqvae.get_layer("encoder")
quantizer = vqvae_trainer.vqvae.get_layer("vector_quantizer")
encoded_outputs = encoder.predict(test_images)
flat_enc_outputs = encoded_outputs.reshape(-1, encoded_outputs.shape[-1])
codebook_indices = quantizer.get_code_indices(flat_enc_outputs)
codebook_indices = codebook_indices.numpy().reshape(encoded_outputs.shape[:-1])
for i in range(len(test_images)):
plt.subplot(1, 2, 1)
plt.imshow(test_images[i].squeeze() + 0.5)
plt.title("Original")
plt.axis("off")
plt.subplot(1, 2, 2)
plt.imshow(codebook_indices[i])
plt.title("Code")
plt.axis("off")
plt.show()
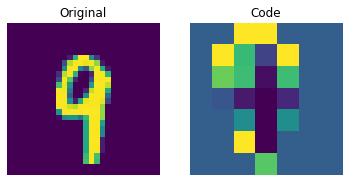


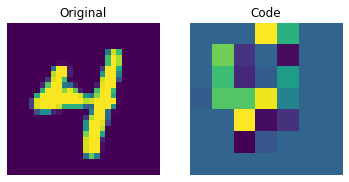
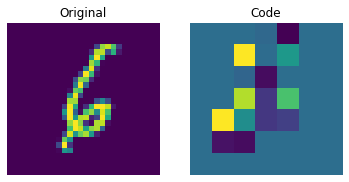
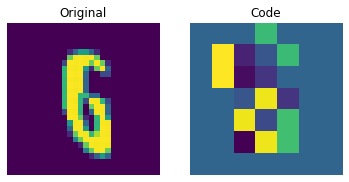
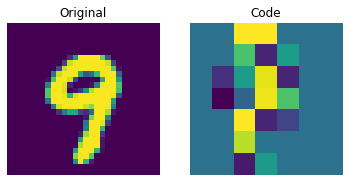


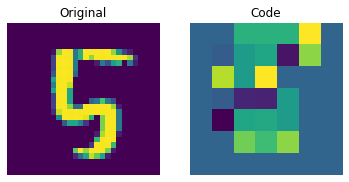
上图显示离散码已经能够捕捉到数据集中的一些规律。那么,我们如何从这个码本中采样来创建新图像呢?由于这些码是离散的,并且我们对它们施加了分类分布,所以在我们能够生成可以提供给解码器的有意义的序列之前,我们还不能使用它们来生成任何有意义的内容。作者使用 PixelCNN 来训练这些码,以便它们可以作为强大的先验来生成新样本。PixelCNN 由 van der Oord 等人在 Conditional Image Generation with PixelCNN Decoders 中提出。我们将从 van der Oord 等人的此示例中借用代码。我们从这个 PixelCNN 示例中借用实现。它是一个自回归生成模型,其输出条件于之前的输出。换句话说,PixelCNN 是逐像素生成图像的。然而,在此示例的用途中,它的任务是生成码本索引而不是像素本身。训练好的 VQ-VAE 解码器用于将 PixelCNN 生成的索引映射回像素空间。
PixelCNN 超参数
num_residual_blocks = 2
num_pixelcnn_layers = 2
pixelcnn_input_shape = encoded_outputs.shape[1:-1]
print(f"Input shape of the PixelCNN: {pixelcnn_input_shape}")
Input shape of the PixelCNN: (7, 7)
此输入形状代表编码器执行的分辨率降低。使用“same”填充,对于每个步长为 2 的卷积层,这会精确地将输出形状的“分辨率”减半。因此,使用这两个层,我们最终会得到一个形状为 7x7 的编码器输出张量(在轴 2 和 3 上),第一个轴是批次大小,最后一个轴是码本嵌入大小。由于自编码器中的量化层将这些 7x7 张量映射到码本的索引,因此 PixelCNN 必须匹配这些输出层轴的大小作为输入形状。此架构的 PixelCNN 的任务是生成可能的 7x7 码本索引排列。
请注意,在更大尺寸的图像域中,这个形状需要与码本大小一起进行优化。由于 PixelCNN 是自回归的,它需要按顺序遍历每个码本索引才能从码本生成新图像。每个步长为 2(或者更准确地说,是步长 (2, 2))的卷积层会将图像生成时间缩短四倍。但请注意,这部分可能有一个下限:当用于重建图像的码的数量太小时,它没有足够的信息供解码器表示图像中的细节级别,因此输出质量会下降。这至少可以在一定程度上通过使用更大的码本来解决。由于图像生成过程的自回归部分使用码本索引,因此使用更大的码本在性能上的损失要小得多,因为从更大的码本中查找较大尺寸的码所需的时间比遍历更大的码本索引序列要小得多,尽管码本的大小确实会影响可以通过图像生成过程传递的批次大小。找到这个权衡的甜蜜点可能需要一些架构调整,并且很可能因数据集而异。
PixelCNN 模型
大部分内容来自此示例。
注意事项
感谢Rein van 't Veer通过文字编辑和少量代码清理改进了此示例。
# The first layer is the PixelCNN layer. This layer simply
# builds on the 2D convolutional layer, but includes masking.
class PixelConvLayer(layers.Layer):
def __init__(self, mask_type, **kwargs):
super().__init__()
self.mask_type = mask_type
self.conv = layers.Conv2D(**kwargs)
def build(self, input_shape):
# Build the conv2d layer to initialize kernel variables
self.conv.build(input_shape)
# Use the initialized kernel to create the mask
kernel_shape = self.conv.kernel.get_shape()
self.mask = np.zeros(shape=kernel_shape)
self.mask[: kernel_shape[0] // 2, ...] = 1.0
self.mask[kernel_shape[0] // 2, : kernel_shape[1] // 2, ...] = 1.0
if self.mask_type == "B":
self.mask[kernel_shape[0] // 2, kernel_shape[1] // 2, ...] = 1.0
def call(self, inputs):
self.conv.kernel.assign(self.conv.kernel * self.mask)
return self.conv(inputs)
# Next, we build our residual block layer.
# This is just a normal residual block, but based on the PixelConvLayer.
class ResidualBlock(keras.layers.Layer):
def __init__(self, filters, **kwargs):
super().__init__(**kwargs)
self.conv1 = keras.layers.Conv2D(
filters=filters, kernel_size=1, activation="relu"
)
self.pixel_conv = PixelConvLayer(
mask_type="B",
filters=filters // 2,
kernel_size=3,
activation="relu",
padding="same",
)
self.conv2 = keras.layers.Conv2D(
filters=filters, kernel_size=1, activation="relu"
)
def call(self, inputs):
x = self.conv1(inputs)
x = self.pixel_conv(x)
x = self.conv2(x)
return keras.layers.add([inputs, x])
pixelcnn_inputs = keras.Input(shape=pixelcnn_input_shape, dtype=tf.int32)
ohe = tf.one_hot(pixelcnn_inputs, vqvae_trainer.num_embeddings)
x = PixelConvLayer(
mask_type="A", filters=128, kernel_size=7, activation="relu", padding="same"
)(ohe)
for _ in range(num_residual_blocks):
x = ResidualBlock(filters=128)(x)
for _ in range(num_pixelcnn_layers):
x = PixelConvLayer(
mask_type="B",
filters=128,
kernel_size=1,
strides=1,
activation="relu",
padding="valid",
)(x)
out = keras.layers.Conv2D(
filters=vqvae_trainer.num_embeddings, kernel_size=1, strides=1, padding="valid"
)(x)
pixel_cnn = keras.Model(pixelcnn_inputs, out, name="pixel_cnn")
pixel_cnn.summary()
Model: "pixel_cnn"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
input_9 (InputLayer) [(None, 7, 7)] 0
_________________________________________________________________
tf.one_hot (TFOpLambda) (None, 7, 7, 128) 0
_________________________________________________________________
pixel_conv_layer (PixelConvL (None, 7, 7, 128) 802944
_________________________________________________________________
residual_block (ResidualBloc (None, 7, 7, 128) 98624
_________________________________________________________________
residual_block_1 (ResidualBl (None, 7, 7, 128) 98624
_________________________________________________________________
pixel_conv_layer_3 (PixelCon (None, 7, 7, 128) 16512
_________________________________________________________________
pixel_conv_layer_4 (PixelCon (None, 7, 7, 128) 16512
_________________________________________________________________
conv2d_21 (Conv2D) (None, 7, 7, 128) 16512
=================================================================
Total params: 1,049,728
Trainable params: 1,049,728
Non-trainable params: 0
_________________________________________________________________
准备数据以训练 PixelCNN
我们将训练 PixelCNN 来学习离散码的分类分布。首先,我们将使用我们刚刚训练好的编码器和向量量化器生成码索引。我们的训练目标是最小化这些索引与 PixelCNN 输出之间的交叉熵损失。在这里,类别数量等于我们码本中的嵌入数量(在本例中为 128)。PixelCNN 模型被训练来学习一个分布(而不是最小化 L1/L2 损失),这就是它获得生成能力的原因。
# Generate the codebook indices.
encoded_outputs = encoder.predict(x_train_scaled)
flat_enc_outputs = encoded_outputs.reshape(-1, encoded_outputs.shape[-1])
codebook_indices = quantizer.get_code_indices(flat_enc_outputs)
codebook_indices = codebook_indices.numpy().reshape(encoded_outputs.shape[:-1])
print(f"Shape of the training data for PixelCNN: {codebook_indices.shape}")
Shape of the training data for PixelCNN: (60000, 7, 7)
PixelCNN 训练
pixel_cnn.compile(
optimizer=keras.optimizers.Adam(3e-4),
loss=keras.losses.SparseCategoricalCrossentropy(from_logits=True),
metrics=["accuracy"],
)
pixel_cnn.fit(
x=codebook_indices,
y=codebook_indices,
batch_size=128,
epochs=30,
validation_split=0.1,
)
Epoch 1/30
422/422 [==============================] - 4s 8ms/step - loss: 1.8550 - accuracy: 0.5959 - val_loss: 1.3127 - val_accuracy: 0.6268
Epoch 2/30
422/422 [==============================] - 3s 7ms/step - loss: 1.2207 - accuracy: 0.6402 - val_loss: 1.1722 - val_accuracy: 0.6482
Epoch 3/30
422/422 [==============================] - 3s 7ms/step - loss: 1.1412 - accuracy: 0.6536 - val_loss: 1.1313 - val_accuracy: 0.6552
Epoch 4/30
422/422 [==============================] - 3s 7ms/step - loss: 1.1060 - accuracy: 0.6601 - val_loss: 1.1058 - val_accuracy: 0.6596
Epoch 5/30
422/422 [==============================] - 3s 7ms/step - loss: 1.0828 - accuracy: 0.6646 - val_loss: 1.1020 - val_accuracy: 0.6603
Epoch 6/30
422/422 [==============================] - 3s 7ms/step - loss: 1.0649 - accuracy: 0.6682 - val_loss: 1.0809 - val_accuracy: 0.6638
Epoch 7/30
422/422 [==============================] - 3s 7ms/step - loss: 1.0515 - accuracy: 0.6710 - val_loss: 1.0712 - val_accuracy: 0.6659
Epoch 8/30
422/422 [==============================] - 3s 7ms/step - loss: 1.0406 - accuracy: 0.6733 - val_loss: 1.0647 - val_accuracy: 0.6671
Epoch 9/30
422/422 [==============================] - 3s 7ms/step - loss: 1.0312 - accuracy: 0.6752 - val_loss: 1.0633 - val_accuracy: 0.6674
Epoch 10/30
422/422 [==============================] - 3s 7ms/step - loss: 1.0235 - accuracy: 0.6771 - val_loss: 1.0554 - val_accuracy: 0.6695
Epoch 11/30
422/422 [==============================] - 3s 7ms/step - loss: 1.0162 - accuracy: 0.6788 - val_loss: 1.0518 - val_accuracy: 0.6694
Epoch 12/30
422/422 [==============================] - 3s 7ms/step - loss: 1.0105 - accuracy: 0.6799 - val_loss: 1.0541 - val_accuracy: 0.6693
Epoch 13/30
422/422 [==============================] - 3s 7ms/step - loss: 1.0050 - accuracy: 0.6811 - val_loss: 1.0481 - val_accuracy: 0.6705
Epoch 14/30
422/422 [==============================] - 3s 7ms/step - loss: 1.0011 - accuracy: 0.6820 - val_loss: 1.0462 - val_accuracy: 0.6709
Epoch 15/30
422/422 [==============================] - 3s 7ms/step - loss: 0.9964 - accuracy: 0.6831 - val_loss: 1.0459 - val_accuracy: 0.6709
Epoch 16/30
422/422 [==============================] - 3s 7ms/step - loss: 0.9922 - accuracy: 0.6840 - val_loss: 1.0444 - val_accuracy: 0.6704
Epoch 17/30
422/422 [==============================] - 3s 7ms/step - loss: 0.9884 - accuracy: 0.6848 - val_loss: 1.0405 - val_accuracy: 0.6725
Epoch 18/30
422/422 [==============================] - 3s 7ms/step - loss: 0.9846 - accuracy: 0.6859 - val_loss: 1.0400 - val_accuracy: 0.6722
Epoch 19/30
422/422 [==============================] - 3s 7ms/step - loss: 0.9822 - accuracy: 0.6864 - val_loss: 1.0394 - val_accuracy: 0.6728
Epoch 20/30
422/422 [==============================] - 3s 7ms/step - loss: 0.9787 - accuracy: 0.6872 - val_loss: 1.0393 - val_accuracy: 0.6717
Epoch 21/30
422/422 [==============================] - 3s 7ms/step - loss: 0.9761 - accuracy: 0.6878 - val_loss: 1.0398 - val_accuracy: 0.6725
Epoch 22/30
422/422 [==============================] - 3s 7ms/step - loss: 0.9733 - accuracy: 0.6884 - val_loss: 1.0376 - val_accuracy: 0.6726
Epoch 23/30
422/422 [==============================] - 3s 7ms/step - loss: 0.9708 - accuracy: 0.6890 - val_loss: 1.0352 - val_accuracy: 0.6732
Epoch 24/30
422/422 [==============================] - 3s 7ms/step - loss: 0.9685 - accuracy: 0.6894 - val_loss: 1.0369 - val_accuracy: 0.6723
Epoch 25/30
422/422 [==============================] - 3s 7ms/step - loss: 0.9660 - accuracy: 0.6901 - val_loss: 1.0384 - val_accuracy: 0.6733
Epoch 26/30
422/422 [==============================] - 3s 7ms/step - loss: 0.9638 - accuracy: 0.6908 - val_loss: 1.0355 - val_accuracy: 0.6728
Epoch 27/30
422/422 [==============================] - 3s 7ms/step - loss: 0.9619 - accuracy: 0.6912 - val_loss: 1.0325 - val_accuracy: 0.6739
Epoch 28/30
422/422 [==============================] - 3s 7ms/step - loss: 0.9594 - accuracy: 0.6917 - val_loss: 1.0334 - val_accuracy: 0.6736
Epoch 29/30
422/422 [==============================] - 3s 7ms/step - loss: 0.9582 - accuracy: 0.6920 - val_loss: 1.0366 - val_accuracy: 0.6733
Epoch 30/30
422/422 [==============================] - 3s 7ms/step - loss: 0.9561 - accuracy: 0.6926 - val_loss: 1.0336 - val_accuracy: 0.6728
<tensorflow.python.keras.callbacks.History at 0x7f95838ef750>
通过更多的训练和超参数调整,我们可以改进这些分数。
码本采样
现在我们的 PixelCNN 已经训练好,我们可以从它的输出中采样不同的码,并将它们传递给我们的解码器来生成新图像。
# Create a mini sampler model.
inputs = layers.Input(shape=pixel_cnn.input_shape[1:])
outputs = pixel_cnn(inputs, training=False)
categorical_layer = tfp.layers.DistributionLambda(tfp.distributions.Categorical)
outputs = categorical_layer(outputs)
sampler = keras.Model(inputs, outputs)
我们现在构建一个用于生成图像的先验。在这里,我们将生成 10 张图像。
# Create an empty array of priors.
batch = 10
priors = np.zeros(shape=(batch,) + (pixel_cnn.input_shape)[1:])
batch, rows, cols = priors.shape
# Iterate over the priors because generation has to be done sequentially pixel by pixel.
for row in range(rows):
for col in range(cols):
# Feed the whole array and retrieving the pixel value probabilities for the next
# pixel.
probs = sampler.predict(priors)
# Use the probabilities to pick pixel values and append the values to the priors.
priors[:, row, col] = probs[:, row, col]
print(f"Prior shape: {priors.shape}")
Prior shape: (10, 7, 7)
我们现在可以使用我们的解码器来生成图像。
# Perform an embedding lookup.
pretrained_embeddings = quantizer.embeddings
priors_ohe = tf.one_hot(priors.astype("int32"), vqvae_trainer.num_embeddings).numpy()
quantized = tf.matmul(
priors_ohe.astype("float32"), pretrained_embeddings, transpose_b=True
)
quantized = tf.reshape(quantized, (-1, *(encoded_outputs.shape[1:])))
# Generate novel images.
decoder = vqvae_trainer.vqvae.get_layer("decoder")
generated_samples = decoder.predict(quantized)
for i in range(batch):
plt.subplot(1, 2, 1)
plt.imshow(priors[i])
plt.title("Code")
plt.axis("off")
plt.subplot(1, 2, 2)
plt.imshow(generated_samples[i].squeeze() + 0.5)
plt.title("Generated Sample")
plt.axis("off")
plt.show()

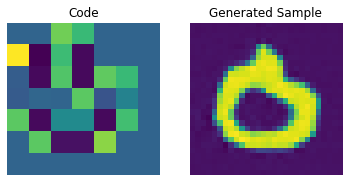
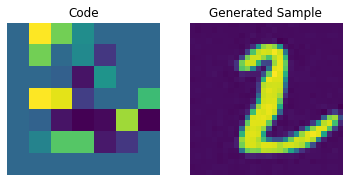
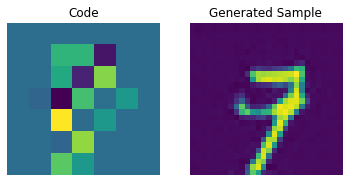
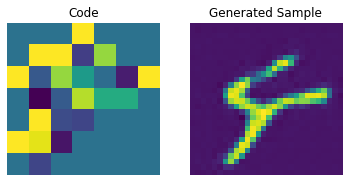
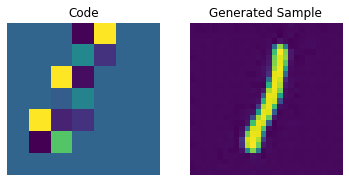
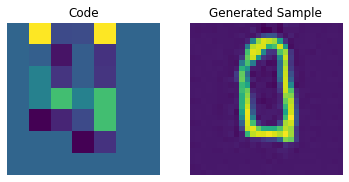
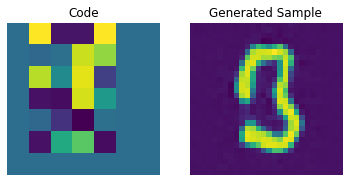
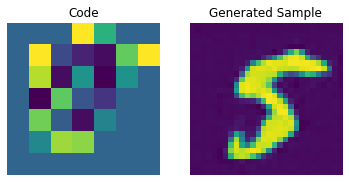

通过调整 PixelCNN,我们可以提高这些生成样本的质量。